题目内容
【题目】已知命题p：若x2+y2＞2，则|x|＞1或|y|＞1；命题q：直线mx-2y-m-2＝0与圆x2+y2-3x+3y+2＝0必有两个不同交点，则下列说法正确的是( )
A. p为真命题 B. p∧(q)为真命题
C. (p)∨q为假命题 D. (p)∨(q)为假命题
【答案】D
【解析】
利用逆否命题的真假与原命题真假可判断p命题的真假，由直线过定点，且点在圆内，可知命题q为真，再一一检验选项即可.
命题p：若x2+y2＞2，则|x|＞1或|y|＞1的逆否命题为：若
且
，则x2+y2
.
显然其逆否命题为真命题，所以命题p为真，p为假命题；
对于命题q，直线mx-2y-m-2＝0，即
，恒过定点(1,-1)，代入圆x2+y2-3x+3y+2＝0可得：
，所以点(1,-1)在圆内，所以直线mx-2y-m-2＝0与圆x2+y2-3x+3y+2＝0必有两个不同交点，命题q为真，q为假命题.
所以(p)∨(q)为假命题，故选D.
【题目】在一次数学测验后，数学老师将某班全体学生（50人）的数学成绩进行初步统计后交给其班主任（如表）.
分数 | 5060 | 60~70 | 70-80 | 80-90 | 90~100 |
人数 | 2 | 6 | 10 | 20 | 12 |
请你帮助这位班主任完成下面的统计分析工作：
（1）列出频率分布表；
（2）画出频率分布直方图及频率折线图；
（3）从频率分布直方图估计出该班同学成绩的众数、中位数和平均数.
【题目】某家庭记录了未使用节水龙头50天的日用水量数据（单位：m3）和使用了节水龙头50天的日用水量数据，得到频数分布表如下：
未使用节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
|
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
（1）在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图：
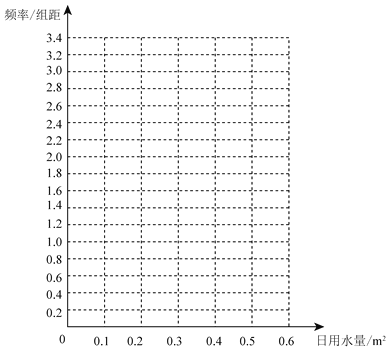
（2）估计该家庭使用节水龙头后，日用水量小于0.35 m3的概率；
（3）估计该家庭使用节水龙头后，一年能节省多少水？（一年按365天计算，同一组中的数据以这组数据所在区间中点的值作代表．）
【题目】西瓜是夏日消暑的好水果，西瓜的销售价格
（单位：千元/吨）与西瓜的年产量
（单位：吨）有关，下表数据为某地区连续6年来西瓜的年产量及对应的西瓜销售价格．
| 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
|
（1）若与有较强的线性相关关系，根据上表提供的数据，用最小二乘法求出与的线性回归直线方程（系数精确到
）；
（2）若每吨西瓜的成本为4810元，假设所有西瓜可以全部卖出，预测当年产量为多少吨 时年利润最大？
参考公式及数据：
p>对于一组数据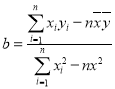
，
，…，
，其回归直线
的斜率和截距的最小二乘估计分别为
，
，其中
，
，
，
． 
