题目内容
【题目】学校或班级举行活动,通常需要张贴海报进行宣传.现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128 dm2,上、下两边各空2 dm,左、右两边各空1 dm.如何设计海报的尺寸,才能使四周空白面积最小?
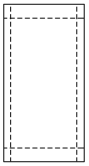
【答案】解:设版心的高为![]() ,则版心的宽为
,则版心的宽为![]() ,此时四周空白面积为:
,此时四周空白面积为:
![]() 可求得当版心高为
可求得当版心高为![]() ,宽为
,宽为![]() ,海报四周空白面积最小.
,海报四周空白面积最小.
【解析】
试题
首先设出高,根据面积可用高将宽表示出来,然后设出空白面积,用高和宽将其表示出来,同时注意高的范围.而后利用导数法判断单调性,可得最值.
试题解析:
设版心的高为![]() ,则版心的宽为
,则版心的宽为![]()
![]() .
.
此时四周空白面积为![]()
求导数得:![]()
令![]() ,解得
,解得![]() (舍去)
(舍去)
于是宽为![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
因此,x=16是函数![]() 的极小值点,也是最小值点。
的极小值点,也是最小值点。
所以当版心高为![]() ,宽为
,宽为![]() 时,能使四周空白面积最小。
时,能使四周空白面积最小。
答:当版心高为![]() ,宽为
,宽为![]() 时,海报四周空白面积最小。
时,海报四周空白面积最小。

练习册系列答案
相关题目
【题目】西瓜是夏日消暑的好水果,西瓜的销售价格![]() (单位:千元/吨)与西瓜的年产量
(单位:千元/吨)与西瓜的年产量![]() (单位:吨)有关,下表数据为某地区连续6年来西瓜的年产量及对应的西瓜销售价格.
(单位:吨)有关,下表数据为某地区连续6年来西瓜的年产量及对应的西瓜销售价格.
| 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
|
(1)若![]() 与
与![]() 有较强的线性相关关系,根据上表提供的数据,用最小二乘法求出
有较强的线性相关关系,根据上表提供的数据,用最小二乘法求出![]() 与
与![]() 的线性回归直线方程(系数精确到
的线性回归直线方程(系数精确到![]() );
);
(2)若每吨西瓜的成本为4810元,假设所有西瓜可以全部卖出,预测当年产量为多少吨 时年利润最大?
参考公式及数据:
p>对于一组数据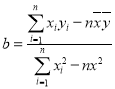 ,
,
