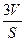题目内容
在平面内,三角形的面积为S,周长为C,则它的内切圆的半径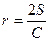 .在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=______________________。
.在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=______________________。
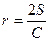 .在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=______________________。
.在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=______________________。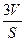
略

练习册系列答案
相关题目
题目内容
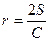 .在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=______________________。
.在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=______________________。