题目内容
14.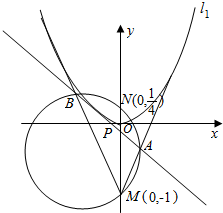 如图,已知抛物线C:y=ax2(a>0)与射线l1:y=2x-1(x≥0)、l2:y=-2x-1(x≤0)均只有一个公共点,过定点M(0,-1)和N(0,$\frac{1}{4}$)的动圆分别与l1、l2交于点A、B,直线AB与x轴交于点P.
如图,已知抛物线C:y=ax2(a>0)与射线l1:y=2x-1(x≥0)、l2:y=-2x-1(x≤0)均只有一个公共点,过定点M(0,-1)和N(0,$\frac{1}{4}$)的动圆分别与l1、l2交于点A、B,直线AB与x轴交于点P.(1)求实数a及$\overrightarrow{NP}$•$\overrightarrow{AB}$的值;
(2)试判断:|MA|+|MB|是否为定值?若是,求出该定值;若不是,说明理由.
分析 (1)联立$\left\{\begin{array}{l}{y=a{x}^{2}}\\{y=2x-1}\end{array}\right.$得:ax2-2x+1=0由△=0求得a,求出P,A,B坐标求得$\overrightarrow{NP}$•$\overrightarrow{AB}$的值.
(2)由第(1)问轻易求得|MA|+|MB|是定值.
解答 解:(1)联立$\left\{\begin{array}{l}{y=a{x}^{2}}\\{y=2x-1}\end{array}\right.$得:ax2-2x+1=0
∴△=4-4a=0,∴a=1.
设动圆Q:(x-t)2$+(y+\frac{3}{8})^{2}={t}^{2}+(\frac{5}{8})^{2}(-\frac{5}{4}<t<\frac{5}{4})$
联立Q,L1:$\left\{\begin{array}{l}{(x-t)^{2}+(y+\frac{3}{8})^{2}={t}^{2}+(\frac{5}{8})^{2}}\\{y=2x-1}\end{array}\right.$
得:A($\frac{2t}{5}+\frac{1}{2},\frac{4t}{5}$).
同理得:B($\frac{2t}{5}-\frac{1}{2},-\frac{4t}{5}$)
∴${l}_{AB}:y-\frac{4t}{5}=\frac{8t}{5}(x-(\frac{2t}{5}+\frac{1}{2}))$令y=0,得P($\frac{2t}{5},0$)
∴$\overrightarrow{NP}•\overrightarrow{AB}=0$
(2)|MA|+|MB|=$\sqrt{\frac{4}{5}}(|t+\frac{5}{4}|+|t-\frac{5}{4}|)=\sqrt{5}$是定值.
设动圆Q:(x-t)2$+(y+\frac{3}{8})^{2}={t}^{2}+(\frac{5}{8})^{2}(-\frac{5}{4}<t<\frac{5}{4})$,圆与l1,l2相切时取得等号.
点评 本题主要考查了直线与圆锥曲线的综合问题---定值问题.属于中档题型,在高考中经常考到.

| 学科 | 数学 | 信息 | 物理 | 化学 | 生物 |
| 北大 | 4 | 2 | 5 | 4 | 1 |
| 清华 | 2 | 1 | 0 | 4 | 2 |
| A. | $\frac{5}{12}$ | B. | $\frac{1}{5}$ | C. | $\frac{12}{25}$ | D. | $\frac{43}{100}$ |
 设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且过点M(0,2).
设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且过点M(0,2).