题目内容
19.高考将至,凭借在五大学科竞赛的卓越表现,我校共有25人获得北大、清华保送及降分录取优惠政策,具体人数如右下表.若随机从这25人中任选2人做经验交流,在已知恰有1人获得北大优惠政策而另1人获得清华优惠政策的条件下,至少有1人是参加数学竞赛的概率为( )| 学科 | 数学 | 信息 | 物理 | 化学 | 生物 |
| 北大 | 4 | 2 | 5 | 4 | 1 |
| 清华 | 2 | 1 | 0 | 4 | 2 |
| A. | $\frac{5}{12}$ | B. | $\frac{1}{5}$ | C. | $\frac{12}{25}$ | D. | $\frac{43}{100}$ |
分析 先求出恰有1人获得北大优惠政策而另1人获得清华优惠政策的种数,再分类求出至少有1人是参加数学竞赛种数,根据概率公式计算即可得到.
解答 解:其中北大保送生有4+2+5+4+1=16人,清华保送生有2+1+0+4+2=9人,
恰有1人获得北大优惠政策而另1人获得清华优惠政策的有C161C91=144种,
故至少有1人是参加数学竞赛种数为C41C71+C21C121+C21C41=28+24+8=60种,
故至少有1人是参加数学竞赛的概率P=$\frac{60}{144}$=$\frac{5}{12}$.
故选:A.
点评 本题考查了古典概型概率问题,以及排列组合的问题,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
8.已知函数f(x)=$\left\{\begin{array}{l}{\frac{1}{x+2},-1≤x≤0}\\{{x}^{2}-2x,0<x≤1}\end{array}\right.$,若f(2m-1)<$\frac{1}{2}$,则m的取值范围是( )
| A. | m$>\frac{1}{2}$ | B. | m$<\frac{1}{2}$ | C. | 0≤m$<\frac{1}{2}$ | D. | $\frac{1}{2}<m≤1$ |
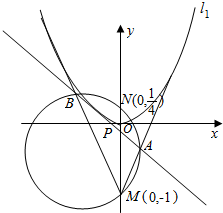 如图,已知抛物线C:y=ax2(a>0)与射线l1:y=2x-1(x≥0)、l2:y=-2x-1(x≤0)均只有一个公共点,过定点M(0,-1)和N(0,$\frac{1}{4}$)的动圆分别与l1、l2交于点A、B,直线AB与x轴交于点P.
如图,已知抛物线C:y=ax2(a>0)与射线l1:y=2x-1(x≥0)、l2:y=-2x-1(x≤0)均只有一个公共点,过定点M(0,-1)和N(0,$\frac{1}{4}$)的动圆分别与l1、l2交于点A、B,直线AB与x轴交于点P.


