题目内容
5.已知函数f(x)=ex-ax有两个零点x1、x2(x1<x2),求证:x1+x2<2lna.分析 利用函数零点的性质,结合函数单调性和导数之间的关系,构造函数,利用导数进行转化即可证明不等式.
解答 解:∵f(x)有两个相异零点,
∴设${e}^{{x}_{1}}$=ax1,${e}^{{x}_{2}}$=ax2,①
即${e}^{{x}_{1}}$${e}^{{x}_{2}}$=${e}^{{x}_{1}+{x}_{2}}$=a2x1x2,
而:x1+x2<2lna,等价于:${e}^{{x}_{1}+{x}_{2}}$<e2lna=${e}^{ln{a}^{2}}$=a2,
即a2x1x2<a2,
则等价为x1x2<1
函数的f(x)的导数f′(x)=ex-a,
若a≤0,则f′(x)=ex-a>0,还是单调递增,则不满足条件.
则a>0,
由f′(x)>0得x>lna,
由f′(x)<0得x<lna,
即当x=lna时,还是f(x)取得极小值同时也是最小值f(lna)=elna-alna=a(1-lna),
∵f(x)有两个零点,∴a(1-lna)<0,
即1-lna<0,则lna>1,即a>e.
要证x1+x2<2lna,则只需要x2<2lna-x1,
又x2>lna,则只需要证明f(x2)<f(2lna-x1),
即证f(2lna-x1)>f(x2)=0=f(x1),
令g(x)=f(2lna-x)-f(x),(x<lna),
则g(x)=e2lna-x-a(2lna-x)-ex+ax,
g′(x)=-a2e-x+a-ex+a=$\frac{-{a}^{2}+2a{e}^{x}-{e}^{2x}}{{e}^{x}}$=-$\frac{({e}^{x}-a)^{2}}{{e}^{x}}$≤0,
即g(x)在(-∞,lna]上单调递减,
即g(x)>g(lna)=0,
则命题成立.
点评 本题主要考查函数单调性和导数之间的关系和应用,综合性较强,运算量较大.

| A. | (0,+∞) | B. | (0,1) | C. | [$\frac{1}{2}$,1) | D. | [$\frac{1}{2}$,2] |
| A. | 若命题p:?x0∈R,使得x02-x0+1<0,则¬p:?x∈R,都有x2-x+1≥0. | |
| B. | 存在无数个α、β∈R,使得等式sin(α-β)=sinαcosβ+cosαsinβ成立 | |
| C. | 命题“在△ABC中,若sinA=sinB,则A=B”的逆否命题是真命题 | |
| D. | “p∧q为真”是“p∨q为真”的必要不充分条件 |
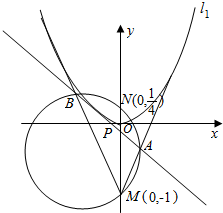 如图,已知抛物线C:y=ax2(a>0)与射线l1:y=2x-1(x≥0)、l2:y=-2x-1(x≤0)均只有一个公共点,过定点M(0,-1)和N(0,$\frac{1}{4}$)的动圆分别与l1、l2交于点A、B,直线AB与x轴交于点P.
如图,已知抛物线C:y=ax2(a>0)与射线l1:y=2x-1(x≥0)、l2:y=-2x-1(x≤0)均只有一个公共点,过定点M(0,-1)和N(0,$\frac{1}{4}$)的动圆分别与l1、l2交于点A、B,直线AB与x轴交于点P.