题目内容
6．不等式|x+2|＜3的解集是（-5，1），不等式|2x-1|≥3的解集是（-∞，-1]∪[2，+∞）．分析 直接利用绝对值的几何意义求解即可．
解答 解：由绝对值的几何意义可知：不等式|x+2|＜3的解集是（-5，1）．
不等式|2x-1|≥3，即2x-1≤-3或2x-1≥3的解集是（-∞，-1]∪[2，+∞）
故答案为：（-5，1）；（-∞，-1]∪[2，+∞）．
点评 本题考查绝对值不等式的解法，考查计算能力．
练习册系列答案
相关题目
17．下列说法中不正确的是（ ）
| A． | 若命题p：?x0∈R，使得x02-x0+1＜0，则￢p：?x∈R，都有x2-x+1≥0． | |
| B． | 存在无数个α、β∈R，使得等式sin（α-β）=sinαcosβ+cosαsinβ成立 | |
| C． | 命题“在△ABC中，若sinA=sinB，则A=B”的逆否命题是真命题 | |
| D． | “p∧q为真”是“p∨q为真”的必要不充分条件 |
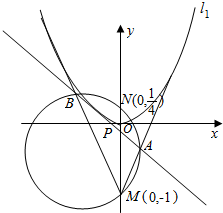如图，已知抛物线C：y=ax2（a＞0）与射线l1：y=2x-1（x≥0）、l2：y=-2x-1（x≤0）均只有一个公共点，过定点M（0，-1）和N（0，$\frac{1}{4}$）的动圆分别与l1、l2交于点A、B，直线AB与x轴交于点P．
16．已知a+2b=2，a＞0，b＞0，则$\frac{1}{2a}$+$\frac{2a}{b}$的最小值是（ ）
| A． | 2 | B． | $\frac{9}{4}$ | C． | $\frac{11}{4}$ | D． | $\frac{9}{2}$ |