题目内容
4.设函数f(x)=$\frac{2{x}^{2}+2x}{{x}^{2}+1}$,求f(x)在[0,1]上的值域.分析 得出f(0)=0,f(1)=2,当0<x<1时,f(x)=2+$\frac{2}{x-1+\frac{2}{x-1}+2}$x∈(0,1),运用对钩函数的单调性求解得出0<2+$\frac{2}{x-1+\frac{2}{x-1}+2}$<2,即可求解值域.
解答  解:∵函数f(x)=$\frac{2{x}^{2}+2x}{{x}^{2}+1}$,
解:∵函数f(x)=$\frac{2{x}^{2}+2x}{{x}^{2}+1}$,
x=0时,f(0)=0,x=1时,f(1)=2,
当0<x<1时,f(x)=2+$\frac{2}{x-1+\frac{2}{x-1}+2}$,
∵x-1+$\frac{2}{x-1}$<-3,
∴x-1$+\frac{2}{x-1}$+2<-1,
∴-1<$\frac{2}{x-1+\frac{2}{x-1}+2}$<0,
即0<2+$\frac{2}{x-1+\frac{2}{x-1}+2}$<2,
综上f(x)在[0,1]上的值域[0,2]
点评 本题考查了分式函数的值域的求解,关键是恒等变形得出不等式条件,运用对钩函数的性质求解,考查了学生的恒等变形能力.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
16.已知a+2b=2,a>0,b>0,则$\frac{1}{2a}$+$\frac{2a}{b}$的最小值是( )
| A. | 2 | B. | $\frac{9}{4}$ | C. | $\frac{11}{4}$ | D. | $\frac{9}{2}$ |
14.函数y=2${\;}^{{x}^{2}}$(x∈R)满足( )
| A. | 在(-∞,+∞)上是增函数 | |
| B. | 在(-∞,+∞)上是减函数 | |
| C. | 在(-∞,0]上是增函数,在[0,+∞)上是减函数 | |
| D. | 在(-∞,0]上是减函数,在[0,+∞)上是增函数 |
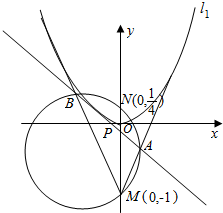 如图,已知抛物线C:y=ax2(a>0)与射线l1:y=2x-1(x≥0)、l2:y=-2x-1(x≤0)均只有一个公共点,过定点M(0,-1)和N(0,$\frac{1}{4}$)的动圆分别与l1、l2交于点A、B,直线AB与x轴交于点P.
如图,已知抛物线C:y=ax2(a>0)与射线l1:y=2x-1(x≥0)、l2:y=-2x-1(x≤0)均只有一个公共点,过定点M(0,-1)和N(0,$\frac{1}{4}$)的动圆分别与l1、l2交于点A、B,直线AB与x轴交于点P.