题目内容
9.已知函数f(x)=2sin(ωx+$\frac{π}{6}$)-1(ω>0)的最小正周期为3π.(1)试求函数y=f(x)(x∈R)图象的对称中心坐标;
(2)在△ABC中,若f(C)=1,且2sin2B=cosB+cos(A-C),求sinA的值.
分析 (1)由条件利用正弦函数的周期性求得ω的值,可得f(x)的解析式,再根据正弦函数图象的对称性求得函数y=f(x)(x∈R)图象的对称中心坐标.
(2)由f(C)=1求得C=$\frac{π}{2}$,再利用同角三角函数的基本关系的应用,诱导公式,求得sinA的值.
解答 解:(1)由于函数f(x)=2sin(ωx+$\frac{π}{6}$)-1(ω>0)的最小正周期为$\frac{2π}{ω}$=3π,∴ω=$\frac{2}{3}$,
f(x)=2sin($\frac{2}{3}$x+$\frac{π}{6}$)-1.
令$\frac{2}{3}$x+$\frac{π}{6}$=kπ,k∈z,求得x=$\frac{3}{2}$kπ-$\frac{π}{4}$,故函数的图象的对称中心为($\frac{3}{2}$kπ-$\frac{π}{4}$,-1),k∈z.
(2)由f(C)=2sin($\frac{2}{3}$C+$\frac{π}{6}$)-1=1,可得sin($\frac{2}{3}$C+$\frac{π}{6}$)=1.
由C∈(0,π),可得$\frac{2}{3}$C+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{5π}{6}$),∴$\frac{2}{3}$C+$\frac{π}{6}$=$\frac{π}{2}$,求得C=$\frac{π}{2}$.
再由2sin2B=cosB+cos(A-C),可得2sin2B=cosB+sinA,即 2cos2A=sinA+sinA,
∴cos2A=sinA,∴1-sin2A=sinA,求得sinA=$\frac{-1+\sqrt{5}}{2}$.
点评 本题主要考查正弦函数的周期性、图象的对称性,同角三角函数的基本关系的应用,诱导公式的应用,属于中档题.

| A. | 若命题p:?x0∈R,使得x02-x0+1<0,则¬p:?x∈R,都有x2-x+1≥0. | |
| B. | 存在无数个α、β∈R,使得等式sin(α-β)=sinαcosβ+cosαsinβ成立 | |
| C. | 命题“在△ABC中,若sinA=sinB,则A=B”的逆否命题是真命题 | |
| D. | “p∧q为真”是“p∨q为真”的必要不充分条件 |
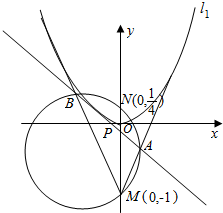 如图,已知抛物线C:y=ax2(a>0)与射线l1:y=2x-1(x≥0)、l2:y=-2x-1(x≤0)均只有一个公共点,过定点M(0,-1)和N(0,$\frac{1}{4}$)的动圆分别与l1、l2交于点A、B,直线AB与x轴交于点P.
如图,已知抛物线C:y=ax2(a>0)与射线l1:y=2x-1(x≥0)、l2:y=-2x-1(x≤0)均只有一个公共点,过定点M(0,-1)和N(0,$\frac{1}{4}$)的动圆分别与l1、l2交于点A、B,直线AB与x轴交于点P.