题目内容
3. 设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且过点M(0,2).
设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且过点M(0,2).(1)求椭圆C的方程;
(2)过椭圆C的右焦点F作直线l与椭圆交于不同的两点A,B,求$\overrightarrow{MA}•\overrightarrow{MB}$的取值范围.
分析 (1)由$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,b=2,a2=b2+c2,联立解出即可;
(2)当l与x轴重合时,直线l:y=0,代入椭圆方程解得x=±2$\sqrt{2}$.即可得出$\overrightarrow{MA}•\overrightarrow{MB}$=-4.
当l与x轴不重合时,设直线l的方程为:my=x-2,A(x1,y1),B(x2,y2).与椭圆方程联立化为(2+m2)y2+4my-4=0,利用根与系数的关系可得$\overrightarrow{MA}•\overrightarrow{MB}$=(x1,y1-2)•(x2,y2-2)=-4+$\frac{8m+20}{2+{m}^{2}}$,
令2m+5=t,解得m=$\frac{t-5}{2}$.可得$\overrightarrow{MA}•\overrightarrow{MB}$=-4+$\frac{32t}{{t}^{2}-10t+33}$=f(t).对t分类讨论,利用基本不等式的性质即可得出.
解答 解:(1)由$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,b=2,a2=b2+c2,
解得b=2,c=2,a=2$\sqrt{2}$.
∴椭圆C的方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$;
(2)当l与x轴重合时,直线l:y=0,代入椭圆方程解得x=±2$\sqrt{2}$.
取$A(-2\sqrt{2},0)$,$B(2\sqrt{2},0)$,∴$\overrightarrow{MA}•\overrightarrow{MB}$=$(-2\sqrt{2},-2)•(2\sqrt{2},-2)$=-8+4=-4.
当l与x轴不重合时,设直线l的方程为:my=x-2,A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{my=x-2}\\{{x}^{2}+2{y}^{2}=8}\end{array}\right.$,化为(2+m2)y2+4my-4=0,
∴y1+y2=$\frac{-4m}{2+{m}^{2}}$,y1y2=$\frac{-4}{2+{m}^{2}}$.
∴$\overrightarrow{MA}•\overrightarrow{MB}$=(x1,y1-2)•(x2,y2-2)=x1x2+(y1-2)(y2-2)=(my1+2)(my2+2)+y1y2-2(y1+y2)+4
=(m2+1)y1y2+(2m-2)(y1+y2)+8
=$\frac{-4({m}^{2}+1)}{2+{m}^{2}}$+$\frac{-4m(2m-2)}{2+{m}^{2}}$+8
=-4+$\frac{8m+20}{2+{m}^{2}}$,
令2m+5=t,解得m=$\frac{t-5}{2}$.
∴$\overrightarrow{MA}•\overrightarrow{MB}$=-4+$\frac{32t}{{t}^{2}-10t+33}$=f(t).
当t=0时,f(t)=-4.
当t>0时,-4<f(t)=-4+$\frac{32}{t+\frac{33}{t}-10}$≤-4+$\frac{32}{2\sqrt{33}-10}$=$6+2\sqrt{33}$,当且仅当t=$\sqrt{33}$,即m=$\frac{\sqrt{33}-5}{2}$时取等号.
当t<0时,-4>f(t)=-4-$\frac{32}{-t+\frac{33}{-t}+10}$≥-4-$\frac{32}{2\sqrt{33}+10}$=6-2$\sqrt{33}$,当且仅当t=-$\sqrt{33}$,即m=$\frac{-\sqrt{33}-5}{2}$时取等号.
综上可得:$\overrightarrow{MA}•\overrightarrow{MB}$取值范围是$[6-2\sqrt{33},6+2\sqrt{33}]$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、数量积运算性质、基本不等式的性质,考查了分类讨论思想方法、推理能力与计算能力,属于难题.

| A. | (0,+∞) | B. | (0,1) | C. | [$\frac{1}{2}$,1) | D. | [$\frac{1}{2}$,2] |
| A. | m$>\frac{1}{2}$ | B. | m$<\frac{1}{2}$ | C. | 0≤m$<\frac{1}{2}$ | D. | $\frac{1}{2}<m≤1$ |
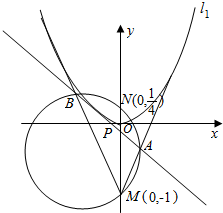 如图,已知抛物线C:y=ax2(a>0)与射线l1:y=2x-1(x≥0)、l2:y=-2x-1(x≤0)均只有一个公共点,过定点M(0,-1)和N(0,$\frac{1}{4}$)的动圆分别与l1、l2交于点A、B,直线AB与x轴交于点P.
如图,已知抛物线C:y=ax2(a>0)与射线l1:y=2x-1(x≥0)、l2:y=-2x-1(x≤0)均只有一个公共点,过定点M(0,-1)和N(0,$\frac{1}{4}$)的动圆分别与l1、l2交于点A、B,直线AB与x轴交于点P.