题目内容
10.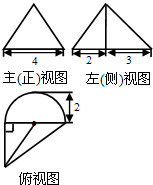 一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )
一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )| A. | $12\sqrt{3}+4\sqrt{3}π$ | B. | $\frac{{4\sqrt{39}}}{3}+\frac{{4\sqrt{3}π}}{3}$ | C. | $12\sqrt{3}+\frac{{4\sqrt{3}π}}{3}$ | D. | $4\sqrt{3}+\frac{{4\sqrt{3}π}}{3}$ |
分析 由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱锥和半圆锥的组合体,求出底面面积,代入棱锥体积公式,可得答案.
解答 解:由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱锥和半圆锥的组合体,
其底面面积S=$\frac{1}{2}×3×4+\frac{1}{2}×π×{2}^{2}$=6+2π,
由主(正)视图是一个等边三角形,
可得该几何体的高h=2$\sqrt{3}$,
故该几何体的体积V=$\frac{1}{3}Sh$=$4\sqrt{3}+\frac{{4\sqrt{3}π}}{3}$,
故选:D
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
20.已知复数(1-i2015)•Z=i2014,则Z的共轭复数在复平面中对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.某人捡到不规则形状的五面体石块,他在每个面上作了记号,投掷了100次,并且记录了每个面落在桌面上的次数(如表),如果再投掷一次,请估计石块的第4面落在桌面上的概率是多少?
| 石块的面 | 1 | 2 | 3 | 4 | 5 |
| 频数 | 32 | 18 | 15 | 13 | 22 |
15.“函数f(x)=lg(ax+1)在(0,+∞)上单调递增”是“a>1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.设x,y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≥2}\\{x≤2}\end{array}\right.$,则z=2x+y+1的最大值为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
20.已知定义在R的函数f(x)满足:
①f(-x)=f(x);
②f(x-2)=f(x);
③?x1,x2∈[0,1](x1≠x2),$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}$>0.
则( )
①f(-x)=f(x);
②f(x-2)=f(x);
③?x1,x2∈[0,1](x1≠x2),$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}$>0.
则( )
| A. | 函数f(x)的图象关于直线x=$\frac{1}{2}$对称 | |
| B. | 函数f(x)的图象关关于点($\frac{1}{2}$,0)对称 | |
| C. | 函数f(x+1)在区间[2013,2014]内单调递增 | |
| D. | 函数f(x+1)的最小正周期为1 |