题目内容
1.一颗骰子A,两面上写的是1,两面上写的是3,一面是4,一面是5;另一颗骰子B,一面是1,一面是2,三面是3,一面是5.如果两个骰子都放在一个袋中,从里面取出一颗骰子并且掷到桌上,问得到1,2,3,4,5的概率分别是$\frac{1}{4}$,$\frac{1}{12}$,$\frac{5}{12}$,$\frac{1}{12}$.分析 确定所有基本事件的个数,其中两个骰子向上点数相同的基本事件的个数,即可求得概率
解答 解:根据题意,本题相当于有12个小球,编号为1的有3个小球,编号为2,4的各有一个小球,编号为3的有5个小球,编号为5的有2个小球,
从中任取一个小球共有12种取法,
取得小球为编号为1的概率为$\frac{3}{12}$=$\frac{1}{4}$,
取得小球为编号为2,4的概率为$\frac{1}{12}$,
取得小球为编号为3的概率为$\frac{5}{12}$,
取得小球为编号为5的概率为$\frac{2}{12}$=$\frac{1}{6}$,
所以得到1,2,3,4,5的概率分别是$\frac{1}{4}$,$\frac{1}{12}$,$\frac{5}{12}$,$\frac{1}{12}$,$\frac{1}{6}$.
故答案为:$\frac{1}{4}$,$\frac{1}{12}$,$\frac{5}{12}$,$\frac{1}{12}$,$\frac{1}{6}$.
点评 本题考查了古典概型的概率问题,转化为摸球问题是关键,属于基础题.

练习册系列答案
相关题目
9.集合A={-1,0,1,2,3},B={-2,-1,0,1},则图中阴影部分表示的集合为( )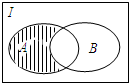

| A. | {-1,0,1} | B. | {2,3} | C. | {-2,2,3} | D. | {-1,0,1,2,3} |
16.执行如图中的程序,如果输出的结果是-4,那么输入的x只可能是( )
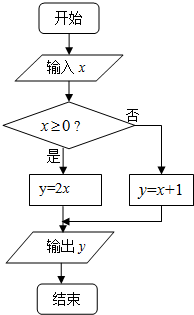

| A. | 3 | B. | 0 | C. | -4 | D. | -5 |
6.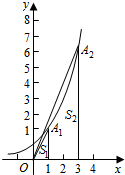 将正奇数组成的数列{an},按下表排成5列:
将正奇数组成的数列{an},按下表排成5列:
(Ⅰ)求第五行到第十行的所有数的和;
(Ⅱ)已知点A1(a1,b1),A2(a2,b2),…,An(an,bn)在指数函数y=2x的图象上,如果,以A1,A2,…,An为一个顶点,x轴y轴为邻边构成的矩形面积为S1,S2,…Sn,求S1+S2+…+Sn的值Tn.
 将正奇数组成的数列{an},按下表排成5列:
将正奇数组成的数列{an},按下表排成5列:| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第一行 | 1 | 3 | 5 | 7 | |
| 第二行 | 15 | 13 | 11 | 9 | |
| 第三行 | 17 | 19 | 21 | 23 | |
| 第四行 | … | … | 27 | 25 |
(Ⅱ)已知点A1(a1,b1),A2(a2,b2),…,An(an,bn)在指数函数y=2x的图象上,如果,以A1,A2,…,An为一个顶点,x轴y轴为邻边构成的矩形面积为S1,S2,…Sn,求S1+S2+…+Sn的值Tn.
13.已知正四棱柱底面边长为1高为2,俯视图是一个面积为1的正方形,则该正四棱锥的正视图的面积不可能等于( )
| A. | 2 | B. | 2.5 | C. | 2$\sqrt{3}$-1 | D. | 2$\sqrt{2}$+1 |
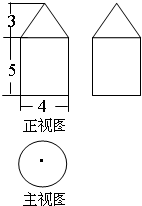
10.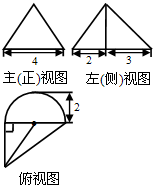 一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )
一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )
 一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )
一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )| A. | $12\sqrt{3}+4\sqrt{3}π$ | B. | $\frac{{4\sqrt{39}}}{3}+\frac{{4\sqrt{3}π}}{3}$ | C. | $12\sqrt{3}+\frac{{4\sqrt{3}π}}{3}$ | D. | $4\sqrt{3}+\frac{{4\sqrt{3}π}}{3}$ |