题目内容
20.已知定义在R的函数f(x)满足:①f(-x)=f(x);
②f(x-2)=f(x);
③?x1,x2∈[0,1](x1≠x2),$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}$>0.
则( )
| A. | 函数f(x)的图象关于直线x=$\frac{1}{2}$对称 | |
| B. | 函数f(x)的图象关关于点($\frac{1}{2}$,0)对称 | |
| C. | 函数f(x+1)在区间[2013,2014]内单调递增 | |
| D. | 函数f(x+1)的最小正周期为1 |
分析 由已知条件得到函数为偶函数,且为以周期为2的周期函数,并在[0,1]上单调递增,再根据图象的平移,即可判断正确答案.
解答 解:由①f(-x)=f(x)可得函数f(x)为偶函数,由②f(x-2)=f(x)可得函数f(x)是以周期为2的周期函数,
由③?x1,x2∈[0,1](x1≠x2),$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}$>0可得函数f(x)在[0,1]上单调递增,
∴故A,B错误,
∵函数f(x+1)是由函数f(x)的图象向左平移一个单位得到的,
∴周期不变,故D错误,
∴函数f(x+1)在区间[2013,2014]内单调性和区间[-1,0]上的单调一致,
∵函数f(x)在[-1,0]上单调递减,
∴函数f(x+1)在[-1,0]上单调递增,
∴函数f(x+1)在区间[2013,2014]内单调递增,
故选:C.
点评 本题考查二楼函数奇偶性,单调性周期性和图象的平移变换,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
10.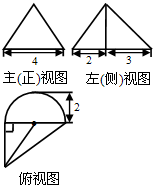 一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )
一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )
 一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )
一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )| A. | $12\sqrt{3}+4\sqrt{3}π$ | B. | $\frac{{4\sqrt{39}}}{3}+\frac{{4\sqrt{3}π}}{3}$ | C. | $12\sqrt{3}+\frac{{4\sqrt{3}π}}{3}$ | D. | $4\sqrt{3}+\frac{{4\sqrt{3}π}}{3}$ |
15.将函数y=sin($2x-\frac{π}{3})$的图象向左平移φ(φ>0)个单位后,所得到的图象对应的函数为奇函数,则φ的最小值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
5.在复平面内,复数$\frac{2i}{1-i}$对应的点的坐标是( )
| A. | (-1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (1,1) |
12.已知0<x1<x2<x3,a=$\frac{{{{log}_2}(2{x_1}+2)}}{x_1},b=\frac{{{{log}_2}(2{x_2}+2)}}{x_2},c=\frac{{{{log}_2}(2{x_3}+2)}}{x_3}$,则a、b、c的大小关系为( )
| A. | c<a<b | B. | b<a<c | C. | a<b<c | D. | c<b<a |
9.已知函数f(x)=$\left\{\begin{array}{l}2lnx-x,x∈(0,2]\\ f(x-2),x∈(2,+∞)\end{array}$,a=log3162,b=$\frac{lg10000}{{{{log}_2}3}}$,则以下结论正确的是( )
| A. | f(a)<f(b)<0 | B. | f(b)<f(a)<0 | C. | 0<f(a)<f(b) | D. | 0<f(b)<f(a) |
9.为了得到函数y=3cos2x的图象,只需把函数$y=3sin(2x+\frac{π}{6})$的图象上所有的点( )
| A. | 向右平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |