题目内容
19.分形几何学是数学家伯努瓦•曼得尔布罗在20世纪70年代创立的一门新的数学学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图甲所示的分形规律可得如图乙所示的一个树形图: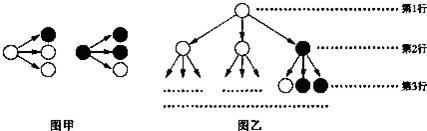
记图乙中第n行白圈的个数为an,则:(Ⅰ)a4=14;(Ⅱ)an=$\frac{{3}^{n-1}+1}{2}$.
分析 (I)根据图甲所示的分形规律,1个白圈分形为2个白圈1个黑圈,1个黑圈分形为1个白圈2个黑圈,根据第三行的数据可求出第四行的白圈的个数;
(Ⅱ)再根据前五行的白圈数乘以2,分别是2,4,10,28,82,即1+1,3+1,9+1,27+1,81+1,可归纳第n行的白圈数
解答 解:(Ⅰ)根据图甲所示的分形规律,1个白圈分形为2个白圈1个黑圈,1个黑圈分形为1个白圈2个黑圈,
记某行白圈x个,黑圈y个为(x,y),
则第一行记为(1,0),
第二行记为(2,1),
第三行记为(5,4),
第四行记为(14,13)
故a4=14
(Ⅱ)各行白圈数乘以2,分别是2,4,10,28,82,即1+1,3+1,9+1,27+1,81+1,
∴第n行的白圈数为$\frac{{3}^{n-1}+1}{2}$,
故答案为:14,$\frac{{3}^{n-1}+1}{2}$
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
9.集合A={-1,0,1,2,3},B={-2,-1,0,1},则图中阴影部分表示的集合为( )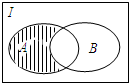

| A. | {-1,0,1} | B. | {2,3} | C. | {-2,2,3} | D. | {-1,0,1,2,3} |
10.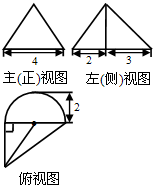 一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )
一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )
 一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )
一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )| A. | $12\sqrt{3}+4\sqrt{3}π$ | B. | $\frac{{4\sqrt{39}}}{3}+\frac{{4\sqrt{3}π}}{3}$ | C. | $12\sqrt{3}+\frac{{4\sqrt{3}π}}{3}$ | D. | $4\sqrt{3}+\frac{{4\sqrt{3}π}}{3}$ |
7.已知四面体ABCD的所有顶点都在球O的球面上,球O的半径为2,AB,AC,AD两两垂直,AB=$\sqrt{2}$,则四面体ABCD体积的最大值为( )
| A. | $\frac{7\sqrt{2}}{6}$ | B. | $\frac{7}{3}$ | C. | 2$\sqrt{2}$ | D. | 2 |
14.设min{p,q}表示p,q两者中的较小者,若函数f(x)=min{3-x,log2x},则满足f(x)≤$\frac{1}{2}$的x的集合为( )
| A. | (0,2]∪[$\frac{5}{2}$,+∞) | B. | [$\sqrt{2}$,$\frac{5}{2}$] | C. | (0,$\sqrt{2}$]∪[$\frac{5}{2}$,+∞) | D. | (0,$\sqrt{2}$)∪($\frac{5}{2}$,+∞) |
4.设函数f(x)=$\frac{1}{2}$cosωx对任意的x∈R,都有f($\frac{π}{6}$-x)=f($\frac{π}{6}$+x),若函数g(x)=-2+3sinωx,则g($\frac{π}{6}$)的值是( )
| A. | 1 | B. | -5或3 | C. | -2 | D. | $\frac{1}{2}$ |
9.已知函数f(x)=$\left\{\begin{array}{l}2lnx-x,x∈(0,2]\\ f(x-2),x∈(2,+∞)\end{array}$,a=log3162,b=$\frac{lg10000}{{{{log}_2}3}}$,则以下结论正确的是( )
| A. | f(a)<f(b)<0 | B. | f(b)<f(a)<0 | C. | 0<f(a)<f(b) | D. | 0<f(b)<f(a) |