��Ŀ����
18�����ں���f��x����������x0��R��ʹf��x0��=x0���������x0Ϊf��x����һ�������㣮�躯��f��x��=ax2+bx+1��a��0��������a=2��b=-2ʱ����f��x���IJ����㣻
������f��x������������IJ�����x1��x2��
��������x1��1��x2ʱ����f��x���ĶԳ���Ϊֱ��x=m����֤��m��$\frac{1}{2}$��
��������|x1|��2��|x1-x2|=2����ʵ��b��ȡֵ��Χ��
���� ����a=2��b=-2ʱ��f��x��=2x2-2x+1�����췽��f��x��=x����ô𰸣�
������f��x������������IJ�����x1��x2����x1��x2�Ƿ���f ��x��=x�����������
��������x1��1��x2ʱ��m=-$\frac{b}{2a}$�����Τ�ﶨ�����ɵ�m��$\frac{1}{2}$��
��������|x1|��2��|x1-x2|=2����Τ�ﶨ���������b�IJ���ʽ�����ʵ��b��ȡֵ��Χ��
��� �⣺���������⣺f��x��=2x2-2x+1=x����2x2-3x+1=0��
���$x=\frac{1}{2}$��1����f��x���IJ�����Ϊ$\frac{1}{2}$��1�� ����5�֣�
�������� ��f ��x������ʽ��m=-$\frac{b}{2a}$��
��g��x��=f ��x��-x=a x2+��b-1��x+1��a��0��
��x1��x2�Ƿ���f ��x��=x�������������x1��1��x2��
��g��1����0⇒a+b��0⇒-$\frac{b}{a}$��1⇒-$\frac{b}{2a}$��$\frac{1}{2}$���� m��$\frac{1}{2}$�� ����9�֣�
��������=��b-1��2-4a��0⇒��b-1��2��4a��
x1+x2=$\frac{1-b}{a}$��x1x2=$\frac{1}{a}$��
��|x1-x2|2=��x1+x2��2-4x1x2=��$\frac{1-b}{a}$��2-$\frac{4}{a}$=22������11�֣�
�ࣨb-1��2=4a+4a2��*��
��|x1-x2|=2��
��x1��x2 �� g��x�� �Գ��� x=$\frac{1-b}{2a}$�ľ��붼Ϊ1��
Ҫʹg��x��=0 ��һ������ ��-2��2����
�� g��x�� �Գ��� x=$\frac{1-b}{2a}$�ʣ�-3��3��������13�֣�
��-3��$\frac{b-1}{2a}$��3⇒a��$\frac{1}{6}$|b-1|��
�Ѵ��� ��*�� �ã���b-1��2��$\frac{2}{3}$|b-1|+$\frac{1}{9}$��b-1��2��
��ã�b��$\frac{1}{4}$�� b��$\frac{7}{4}$��
��b ��ȡֵ��Χ�ǣ���-�ޣ�$\frac{1}{4}$���ȣ� $\frac{7}{4}$��+�ޣ�������15�֣�
���� ���⿼���֪ʶ���Ƕ��κ�����ͼ������ʣ�Τ�ﶨ�����Ƕ��η�������κ��������β���ʽ���ۺ�Ӧ�ã��ѶȽϴ�

 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�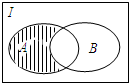
| A�� | {-1��0��1} | B�� | {2��3} | C�� | {-2��2��3} | D�� | {-1��0��1��2��3} |
 ����������ɵ�����{an}�����±��ų�5�У�
����������ɵ�����{an}�����±��ų�5�У�| ��1�� | ��2�� | ��3�� | ��4�� | ��5�� | |
| ��һ�� | 1 | 3 | 5 | 7 | |
| �ڶ��� | 15 | 13 | 11 | 9 | |
| ������ | 17 | 19 | 21 | 23 | |
| ������ | �� | �� | 27 | 25 |
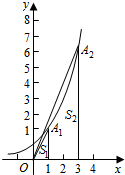
������֪��A1��a1��b1����A2��a2��b2��������An��an��bn����ָ������y=2x��ͼ���ϣ��������A1��A2������AnΪһ�����㣬x��y��Ϊ�ڱ߹��ɵľ������ΪS1��S2����Sn����S1+S2+��+Sn��ֵTn��
| A�� | 2 | B�� | 2.5 | C�� | 2$\sqrt{3}$-1 | D�� | 2$\sqrt{2}$+1 |
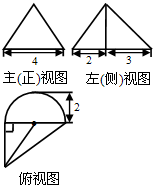 һ�������������ͼ��ͼ��ʾ��������������ͼ��һ���ȱ������Σ����������������Ϊ��������
һ�������������ͼ��ͼ��ʾ��������������ͼ��һ���ȱ������Σ����������������Ϊ��������| A�� | $12\sqrt{3}+4\sqrt{3}��$ | B�� | $\frac{{4\sqrt{39}}}{3}+\frac{{4\sqrt{3}��}}{3}$ | C�� | $12\sqrt{3}+\frac{{4\sqrt{3}��}}{3}$ | D�� | $4\sqrt{3}+\frac{{4\sqrt{3}��}}{3}$ |
| A�� | $\frac{7\sqrt{2}}{6}$ | B�� | $\frac{7}{3}$ | C�� | 2$\sqrt{2}$ | D�� | 2 |