题目内容
已知椭圆
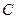 的中心在坐标原点,左顶点
的中心在坐标原点,左顶点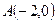 ,离心率
,离心率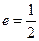 ,
,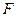 为右焦点,过焦点
为右焦点,过焦点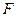 的直线交椭圆
的直线交椭圆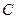 于
于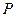 、
、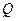 两点(不同于点
两点(不同于点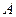 ).
).(Ⅰ)求椭圆
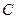 的方程;
的方程;(Ⅱ)当
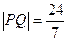 时,求直线PQ的方程;
时,求直线PQ的方程;(Ⅲ)判断
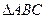 能否成为等边三角形,并说明理由.
能否成为等边三角形,并说明理由.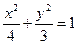 ,
,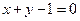 或
或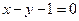 ,不能
,不能解:(Ⅰ)设椭圆方程为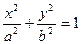 (a>b>0) ,
(a>b>0) ,
由已知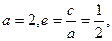
∴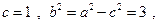 -----------------------------------------2分
-----------------------------------------2分
∴椭圆方程为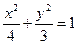 . -------------------------------------------------4分
. -------------------------------------------------4分
(Ⅱ)解法一
椭圆右焦点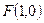 .
.
设直线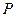
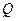 方程为
方程为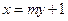 (
(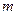 ∈R). ----------------------------------5分
∈R). ----------------------------------5分
由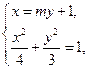 得
得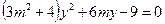 .① -----------6分
.① -----------6分
显然,方程①的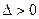 .
.
设 ,则有
,则有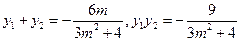 . ----7分
. ----7分
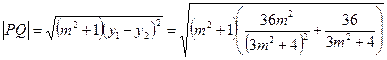
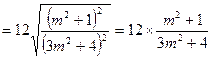 .
.
∵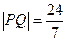 ,
,
∴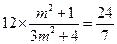 .
.
解得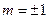 .
.
∴直线PQ 方程为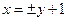 ,即
,即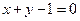 或
或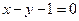 . ----------9分
. ----------9分
解法二:椭圆右焦点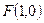 .
.
当直线的斜率不存在时,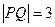 ,不合题意.
,不合题意.
设直线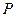
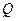 方程为
方程为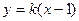 , --------------------------------------5分
, --------------------------------------5分
由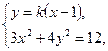 得
得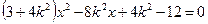 . ① ----6分
. ① ----6分
显然,方程①的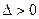 .
.
设 ,则
,则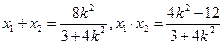 . --------7分
. --------7分


=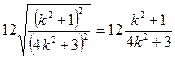 .
.
∵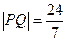 ,
,
∴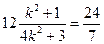 ,解得
,解得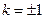 .
.
∴直线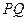 的方程为
的方程为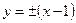 ,即
,即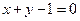 或
或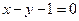 . --------9分
. --------9分
(Ⅲ)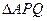 不可能是等边三角形. ---------------------------------------------------11分
不可能是等边三角形. ---------------------------------------------------11分
如果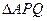 是等边三角形,必有
是等边三角形,必有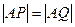 ,
,
∴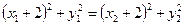 ,
,
∴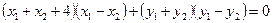 ,
,
∴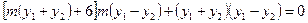 ,
,
∵ ,
,
∴ ,
,
∴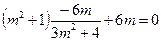 ,
,
∴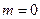 ,或
,或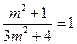 (无解).
(无解).
而当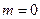 时,
时,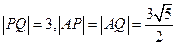 ,不能构成等边三角形.
,不能构成等边三角形.
∴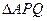 不可能是等边三角形.------------------------------------------------------------14分
不可能是等边三角形.------------------------------------------------------------14分
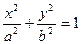 (a>b>0) ,
(a>b>0) ,由已知
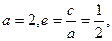
∴
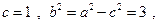 -----------------------------------------2分
-----------------------------------------2分∴椭圆方程为
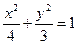 . -------------------------------------------------4分
. -------------------------------------------------4分(Ⅱ)解法一
椭圆右焦点
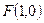 .
.设直线
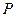
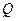 方程为
方程为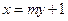 (
(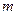 ∈R). ----------------------------------5分
∈R). ----------------------------------5分由
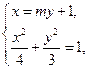 得
得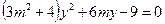 .① -----------6分
.① -----------6分显然,方程①的
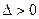 .
.设
 ,则有
,则有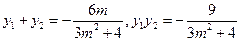 . ----7分
. ----7分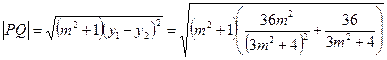
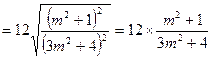 .
.∵
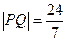 ,
,∴
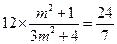 .
.解得
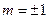 .
.∴直线PQ 方程为
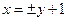 ,即
,即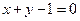 或
或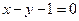 . ----------9分
. ----------9分解法二:椭圆右焦点
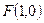 .
.当直线的斜率不存在时,
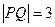 ,不合题意.
,不合题意.设直线
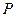
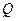 方程为
方程为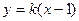 , --------------------------------------5分
, --------------------------------------5分由
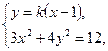 得
得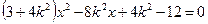 . ① ----6分
. ① ----6分显然,方程①的
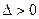 .
.设
 ,则
,则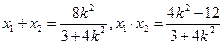 . --------7分
. --------7分

=
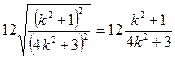 .
.∵
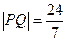 ,
,∴
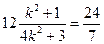 ,解得
,解得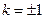 .
.∴直线
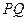 的方程为
的方程为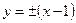 ,即
,即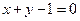 或
或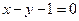 . --------9分
. --------9分(Ⅲ)
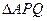 不可能是等边三角形. ---------------------------------------------------11分
不可能是等边三角形. ---------------------------------------------------11分如果
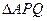 是等边三角形,必有
是等边三角形,必有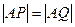 ,
,∴
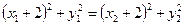 ,
,∴
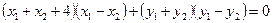 ,
,∴
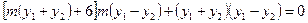 ,
,∵
 ,
,∴
 ,
,∴
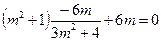 ,
,∴
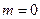 ,或
,或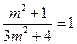 (无解).
(无解).而当
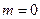 时,
时,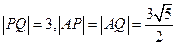 ,不能构成等边三角形.
,不能构成等边三角形.∴
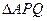 不可能是等边三角形.------------------------------------------------------------14分
不可能是等边三角形.------------------------------------------------------------14分
练习册系列答案
相关题目
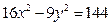 的左、右两个焦点分别为
的左、右两个焦点分别为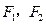 ,点
,点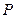 在双曲线上,且
在双曲线上,且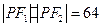 ,求
,求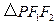 的面积.
的面积.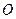 ,焦点在
,焦点在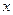 轴上,斜率为
轴上,斜率为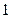 且过椭圆右焦点
且过椭圆右焦点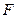 的直线交椭圆于
的直线交椭圆于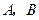 两点,
两点,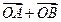 与
与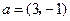 共线.设
共线.设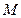 为椭圆上任意一点,且
为椭圆上任意一点,且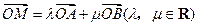 ,证明
,证明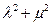 为定值.
为定值.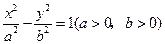 ,
,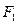 ,
,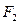 为双曲线的两个焦点,点
为双曲线的两个焦点,点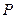 在双曲线上,求
在双曲线上,求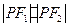 的最小值.
的最小值.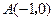 ,
, ,动点
,动点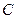 满足
满足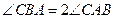 ,求动点
,求动点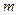 取何值,曲线
取何值,曲线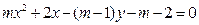 总通过定点.
总通过定点.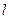 过坐标原点,抛物线
过坐标原点,抛物线 的顶点在原点,焦点在
的顶点在原点,焦点在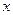 轴正半轴上,若点
轴正半轴上,若点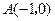 和点
和点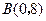 关于
关于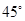 的直线
的直线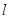 过点
过点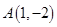 和点
和点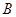 ,点
,点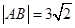 。
。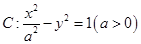 相交于
相交于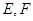 两点,且线段
两点,且线段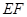 的中点坐标为
的中点坐标为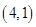 ,求
,求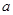 的值;
的值;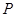 ,当点
,当点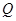 在线段
在线段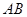 上运动时,称
上运动时,称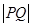 的最小值为
的最小值为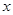 轴上运动,写出点
轴上运动,写出点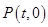 到线段
到线段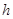 关于
关于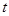 的函数关系式。
的函数关系式。