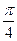题目内容
(本小题满分12分)
已知抛物线方程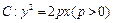 ,点
,点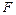 为其焦点,点
为其焦点,点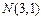 在抛物线
在抛物线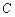 的内部,设点
的内部,设点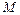 是抛物线
是抛物线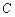 上的任意一点,
上的任意一点,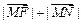 的最小值为4.
的最小值为4.
(1)求抛物线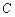 的方程;
的方程;
(2)过点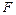 作直线
作直线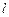 与抛物线
与抛物线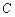 交于不同两点
交于不同两点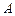 、
、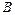 ,与
,与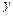 轴交于点
轴交于点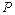 ,且
,且
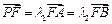 ,试判断
,试判断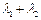 是否为定值?若是定值,求出该定值并证明;若不是定值,
是否为定值?若是定值,求出该定值并证明;若不是定值,
请说明理由.
已知抛物线方程
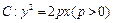 ,点
,点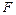 为其焦点,点
为其焦点,点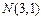 在抛物线
在抛物线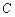 的内部,设点
的内部,设点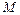 是抛物线
是抛物线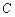 上的任意一点,
上的任意一点,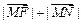 的最小值为4.
的最小值为4.(1)求抛物线
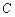 的方程;
的方程;(2)过点
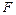 作直线
作直线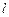 与抛物线
与抛物线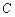 交于不同两点
交于不同两点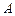 、
、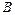 ,与
,与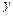 轴交于点
轴交于点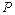 ,且
,且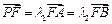 ,试判断
,试判断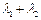 是否为定值?若是定值,求出该定值并证明;若不是定值,
是否为定值?若是定值,求出该定值并证明;若不是定值,请说明理由.
解:(1)准线方程为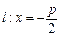 ,点
,点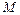 到
到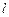 的距离设为
的距离设为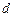 ,
,
由抛物线定义,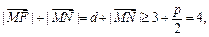 …………………………………………2分
…………………………………………2分
所以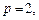
所以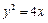 ………………………………………………………………………………4分
………………………………………………………………………………4分
(2)设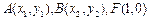
由题意知直线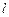 的斜率
的斜率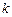 存在且不等于0,
存在且不等于0,
设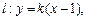 则
则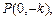
由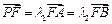 知
知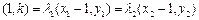

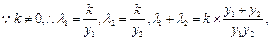 ………………………………………………8分
………………………………………………8分
将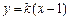 代入
代入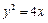 得
得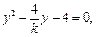
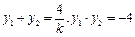
 ……………………………………………………………………10分
……………………………………………………………………10分
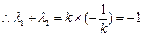 为定值.……………………………………………………………12分
为定值.……………………………………………………………12分
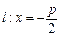 ,点
,点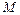 到
到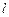 的距离设为
的距离设为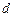 ,
,由抛物线定义,
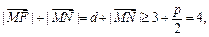 …………………………………………2分
…………………………………………2分所以
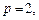
所以
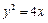 ………………………………………………………………………………4分
………………………………………………………………………………4分(2)设
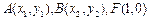
由题意知直线
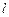 的斜率
的斜率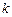 存在且不等于0,
存在且不等于0,设
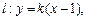 则
则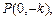
由
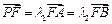 知
知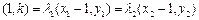

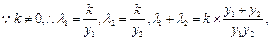 ………………………………………………8分
………………………………………………8分将
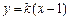 代入
代入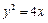 得
得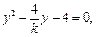
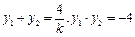
 ……………………………………………………………………10分
……………………………………………………………………10分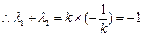 为定值.……………………………………………………………12分
为定值.……………………………………………………………12分略

练习册系列答案
相关题目
 与坐标轴的交点为焦点的抛物线的标准方程为( )
与坐标轴的交点为焦点的抛物线的标准方程为( )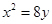 或
或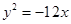
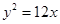
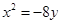 或
或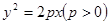 的准线与圆
的准线与圆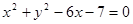 相切,则
相切,则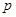 的值为
的值为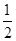
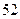 米,拱顶离水平面
米,拱顶离水平面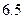 米,水面上有一竹排上放有宽10米、高6米的木箱,问其能否安全通过拱桥?
米,水面上有一竹排上放有宽10米、高6米的木箱,问其能否安全通过拱桥?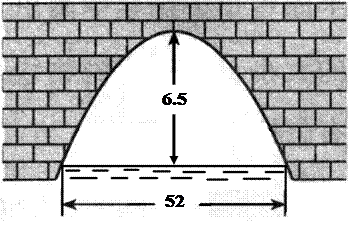
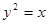 的焦点F,交抛物线于A,B两点,且点A在x轴上方,若直线l的倾斜角
的焦点F,交抛物线于A,B两点,且点A在x轴上方,若直线l的倾斜角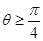 ,则|FA|的取值范围是( )
,则|FA|的取值范围是( )



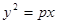 的焦点与椭圆
的焦点与椭圆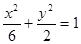 的右焦点重合,则p的值为
的右焦点重合,则p的值为

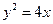 上的两点A、B满足
上的两点A、B满足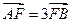 ,则弦AB的中点到准线的距离为____
,则弦AB的中点到准线的距离为____