题目内容
如图,已知球O的面上四点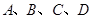 ,DA⊥平面ABC。AB⊥BC,DA=AB=BC=
,DA⊥平面ABC。AB⊥BC,DA=AB=BC=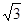 ,则球O的体积等于 。
,则球O的体积等于 。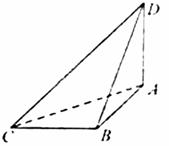
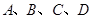 ,DA⊥平面ABC。AB⊥BC,DA=AB=BC=
,DA⊥平面ABC。AB⊥BC,DA=AB=BC=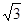 ,则球O的体积等于 。
,则球O的体积等于 。
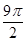
本小题主要考查球的内接几何体体积计算问题。其关键是找出球心,从而确定球的半径。由题意,三角形DAC,三角形DBC都是直角三角形,且有公共斜边。所以DC边的中点就是球心(到D、A、C、B四点距离相等),所以球的半径就是线段DC长度的一半。

练习册系列答案
相关题目
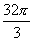 ,则此球的表面积是( )
,则此球的表面积是( ) 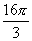
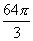
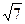 ,球心
,球心 到平面ABC的距离为
到平面ABC的距离为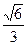 ,则该球的表面积等于 .
,则该球的表面积等于 . ,
,
 ,则正方体的棱长等于 .
,则正方体的棱长等于 .
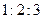 ,则它们的体积之比是_____________。
,则它们的体积之比是_____________。