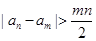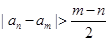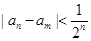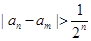题目内容
如果数列 同时满足:(1)各项均不为
同时满足:(1)各项均不为 ,(2)存在常数k, 对任意
,(2)存在常数k, 对任意 都成立,则称这样的数列
都成立,则称这样的数列 为“类等比数列” .由此等比数列必定是“类等比数列” .问:
为“类等比数列” .由此等比数列必定是“类等比数列” .问:
(1)各项均不为0的等差数列 是否为“类等比数列”?说明理由.
是否为“类等比数列”?说明理由.
(2)若数列 为“类等比数列”,且
为“类等比数列”,且 (a,b为常数),是否存在常数λ,使得
(a,b为常数),是否存在常数λ,使得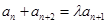 对任意
对任意 都成立?若存在,求出λ;若不存在,请举出反例.
都成立?若存在,求出λ;若不存在,请举出反例.
(3)若数列 为“类等比数列”,且
为“类等比数列”,且 ,
, (a,b为常数),求数列
(a,b为常数),求数列 的前n项之和
的前n项之和 ;数列
;数列 的前n项之和记为
的前n项之和记为 ,求
,求 .
.
 同时满足:(1)各项均不为
同时满足:(1)各项均不为 ,(2)存在常数k, 对任意
,(2)存在常数k, 对任意 都成立,则称这样的数列
都成立,则称这样的数列 为“类等比数列” .由此等比数列必定是“类等比数列” .问:
为“类等比数列” .由此等比数列必定是“类等比数列” .问:(1)各项均不为0的等差数列
 是否为“类等比数列”?说明理由.
是否为“类等比数列”?说明理由.(2)若数列
 为“类等比数列”,且
为“类等比数列”,且 (a,b为常数),是否存在常数λ,使得
(a,b为常数),是否存在常数λ,使得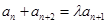 对任意
对任意 都成立?若存在,求出λ;若不存在,请举出反例.
都成立?若存在,求出λ;若不存在,请举出反例.(3)若数列
 为“类等比数列”,且
为“类等比数列”,且 ,
, (a,b为常数),求数列
(a,b为常数),求数列 的前n项之和
的前n项之和 ;数列
;数列 的前n项之和记为
的前n项之和记为 ,求
,求 .
.(1)是,(2)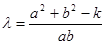 ,(3)
,(3)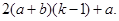
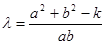 ,(3)
,(3)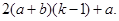
试题分析:(1)解决新定义问题,关键根据“定义”列条件,根据“定义”判断. 因为
 为各项均不为
为各项均不为 的等差数列,故可设
的等差数列,故可设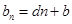 (d、b为常数),由
(d、b为常数),由 得
得 得
得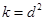 为常数,所以各项均不为0的等差数列
为常数,所以各项均不为0的等差数列 为“类等比数列”,(2)存在性问题,通常从假设存在出发,列等量关系,将是否存在转化为对应方程是否有解. 先从必要条件入手
为“类等比数列”,(2)存在性问题,通常从假设存在出发,列等量关系,将是否存在转化为对应方程是否有解. 先从必要条件入手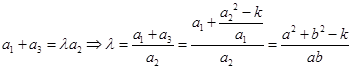 ,再从充分性上证明:因为
,再从充分性上证明:因为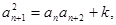 所以
所以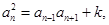 所以
所以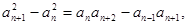 即
即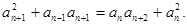 得
得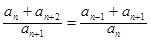 所以
所以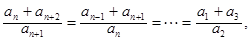
而
 (3)由(2)易得
(3)由(2)易得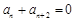 ,
,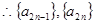 均为公比为
均为公比为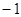 的等比数列,
的等比数列,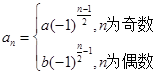 ,
,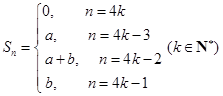 ,
,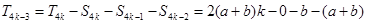
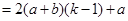
[解] (1)因为
 为各项均不为
为各项均不为 的等差数列,故可设
的等差数列,故可设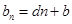 (d、b为常数) 1分
(d、b为常数) 1分由
 得
得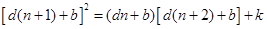 2分
2分得
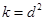 为常数,所以各项均不为0的等差数列
为常数,所以各项均不为0的等差数列 为“类等比数列” 4分
为“类等比数列” 4分(2)存在常数
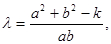 使
使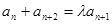 (只给出结论给2分)
(只给出结论给2分)(或从必要条件入手
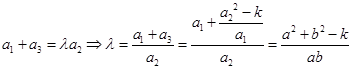 )
)证明如下:因为
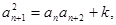 所以
所以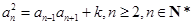
所以
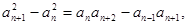 即
即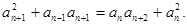 6分
6分由于
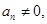 此等式两边同除以
此等式两边同除以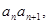
得
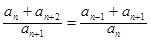 8分
8分所以
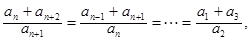
即当
 都有
都有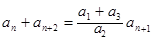
因为
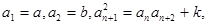 所以
所以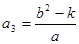
所以

所以对任意
 都有
都有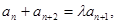 此时
此时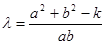 10分
10分(3)
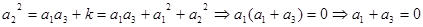 11分
11分
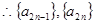 均为公比为
均为公比为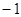 的等比数列 12分
的等比数列 12分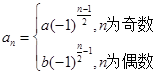 14分
14分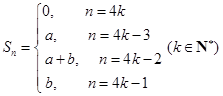 16分
16分
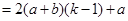 18分
18分
练习册系列答案
相关题目
 )定义为如下数表,且对任意自然数n均有xn+1=
)定义为如下数表,且对任意自然数n均有xn+1=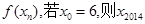 的值为( )
的值为( )
 满足奇数项
满足奇数项 成等差数列
成等差数列 ,而偶数项
,而偶数项 成等比数列
成等比数列 ,且
,且 ,
, 成等差数列,数列
成等差数列,数列 项和为
项和为 .
. ;
;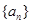 中,
中,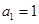 ,对于任意
,对于任意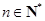 ,都有
,都有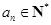 ,
,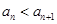 . 设
. 设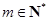 , 记使得
, 记使得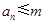 成立的
成立的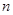 的最大值为
的最大值为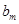 .
.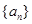 为1,3,5,7,
为1,3,5,7, ,写出
,写出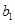 ,
,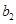 ,
,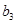 的值;
的值;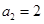 ,求
,求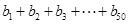 的值;
的值;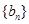 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列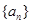 中,已知
中,已知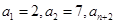 等于
等于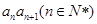 的个位数,则
的个位数,则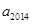 的值是
的值是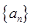 ,定义数列
,定义数列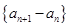 为数列
为数列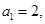
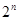 ,则数列
,则数列 .
. 的前n项和
的前n项和 ,则
,则 的值为 ( )
的值为 ( )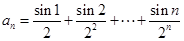 ,则对任意正整数
,则对任意正整数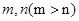 都成立的是( )
都成立的是( )