题目内容
(4分)(2011•福建)商家通常依据“乐观系数准则”确定商品销售价格,及根据商品的最低销售限价a,最高销售限价b(b>a)以及常数x(0<x<1)确定实际销售价格c=a+x(b﹣a),这里,x被称为乐观系数.
经验表明,最佳乐观系数x恰好使得(c﹣a)是(b﹣c)和(b﹣a)的等比中项,据此可得,最佳乐观系数x的值等于 .
经验表明,最佳乐观系数x恰好使得(c﹣a)是(b﹣c)和(b﹣a)的等比中项,据此可得,最佳乐观系数x的值等于 .
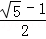
试题分析:根据题设条件,由(c﹣a)是(b﹣c)和(b﹣a)的等比中项,知[x(b﹣a)]2=(b﹣a)2﹣x(b﹣a)2,由此能求出最佳乐观系数x的值.
解:∵c﹣a=x(b﹣a),b﹣c=(b﹣a)﹣x(b﹣a),
(c﹣a)是(b﹣c)和(b﹣a)的等比中项,
∴[x(b﹣a)]2=(b﹣a)2﹣x(b﹣a)2,
∴x2+x﹣1=0,
解得
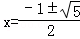 ,
,∵0<x<1,
∴
 .
.故答案为:
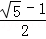 .
.点评:本题考查等比数列的性质和应用,解题时要注意等比中项的计算.

练习册系列答案
相关题目
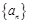 满足:
满足: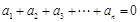 且
且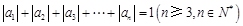 ,则称数列
,则称数列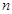 阶“归化数列”.
阶“归化数列”.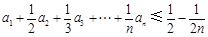 .
. ,设数列
,设数列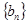 满足
满足  .
.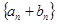 的前
的前 项和为
项和为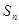 ;
; ,若
,若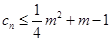 对一切正整数
对一切正整数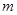 的取值范围.
的取值范围. 通项为
通项为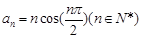 ,则
,则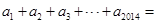 .
. 同时满足:(1)各项均不为
同时满足:(1)各项均不为 ,(2)存在常数k, 对任意
,(2)存在常数k, 对任意 都成立,则称这样的数列
都成立,则称这样的数列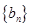 是否为“类等比数列”?说明理由.
是否为“类等比数列”?说明理由.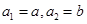 (a,b为常数),是否存在常数λ,使得
(a,b为常数),是否存在常数λ,使得 对任意
对任意 都成立?若存在,求出λ;若不存在,请举出反例.
都成立?若存在,求出λ;若不存在,请举出反例. (a,b为常数),求数列
(a,b为常数),求数列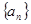 的前n项之和
的前n项之和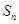 ;数列
;数列 的前n项之和记为
的前n项之和记为 ,求
,求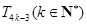 .
. +f(x),x∈R,且f(1)=
+f(x),x∈R,且f(1)= ,则数列{f(n)}(n∈N*)的前20项的和为( )
,则数列{f(n)}(n∈N*)的前20项的和为( )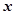 是4和16的等差中项,则
是4和16的等差中项,则