题目内容
对于数列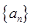 ,定义数列
,定义数列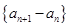 为数列
为数列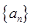 的“差数列”,若
的“差数列”,若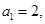
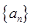 的“差数列”的通项为
的“差数列”的通项为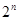 ,则数列
,则数列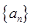 的前n项和
的前n项和 .
.
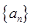 ,定义数列
,定义数列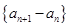 为数列
为数列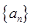 的“差数列”,若
的“差数列”,若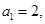
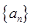 的“差数列”的通项为
的“差数列”的通项为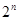 ,则数列
,则数列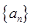 的前n项和
的前n项和 .
.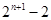
试题分析:由“差数列”定义知:
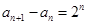 ,
,所以
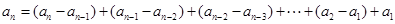
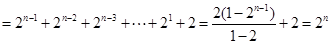
因此

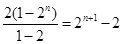 .
.
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
题目内容
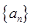 ,定义数列
,定义数列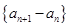 为数列
为数列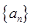 的“差数列”,若
的“差数列”,若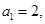
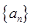 的“差数列”的通项为
的“差数列”的通项为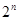 ,则数列
,则数列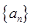 的前n项和
的前n项和 .
.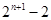
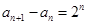 ,
,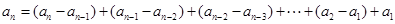
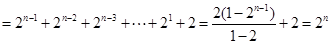

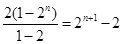 .
.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案