题目内容
下列图象中有一个是函数f（x）=
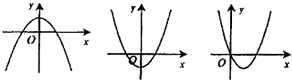
x3+ax2+（a2-1）x+1（a∈R，a≠0）的导数f′（x）的图象，则f（-1）=（ ）
| 1 |
| 3 |
A．
| B．-
| C．
| D．-
|
∵f′（x）=x2+2ax+（a2-1），
∴导函数f′（x）的图象开口向上．
又∵a≠0，
∴f（x）不是偶函数，其图象不关于y轴对称
其图象必为第三张图．由图象特征知f′（0）=0，
且对称轴-a＞0，
∴a=-1．
故f（-1）=-
-1+1=-
．
故选B．
∴导函数f′（x）的图象开口向上．
又∵a≠0，
∴f（x）不是偶函数，其图象不关于y轴对称
其图象必为第三张图．由图象特征知f′（0）=0，
且对称轴-a＞0，
∴a=-1．
故f（-1）=-
| 1 |
| 3 |
| 1 |
| 3 |
故选B．
练习册系列答案
阅读快车系列答案
相关题目
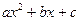，其中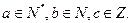
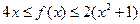恒成立,且存在
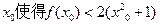成立，求c的值。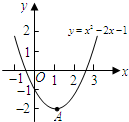
时，函数
取得最小值. 
为偶函数，则
的值是（ ）