题目内容
若f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x,
(1)求f(x)的解析式;
(2)函数y=f(x+a)在区间[-1,3]上不单调,求实数a的取值范围.
(1)求f(x)的解析式;
(2)函数y=f(x+a)在区间[-1,3]上不单调,求实数a的取值范围.
(1)设f(x)=ax2+bx+c(a≠0),
∵f(0)=1,∴c=1,
∴f(x)=ax2+bx+1.
∵f(x+1)-f(x)=2x,
∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2ax+a+b=2x,
∴
,
∴a=1,b=-1,
∴f(x)=x2-x+1.
(2)∵y=f(x+a)=(x+a)2-(x+a)+1=x2+(2a-1)x+a2-a+1 在[-1,3]不单调,
∴二次函数f(x)的对称轴x=-a+
在区间[-1,3]内,
∴-1<-a+
<3,
∴-
<a<
,
∴k的取值范围为{a|-
<a<
}.
∵f(0)=1,∴c=1,
∴f(x)=ax2+bx+1.
∵f(x+1)-f(x)=2x,
∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2ax+a+b=2x,
∴
|
∴a=1,b=-1,
∴f(x)=x2-x+1.
(2)∵y=f(x+a)=(x+a)2-(x+a)+1=x2+(2a-1)x+a2-a+1 在[-1,3]不单调,
∴二次函数f(x)的对称轴x=-a+
| 1 |
| 2 |
∴-1<-a+
| 1 |
| 2 |
∴-
| 5 |
| 2 |
| 3 |
| 2 |
∴k的取值范围为{a|-
| 5 |
| 2 |
| 3 |
| 2 |

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
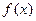 满足
满足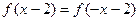 ,且其图象在y轴上的截距为1,在x轴上截得的线段长为
,且其图象在y轴上的截距为1,在x轴上截得的线段长为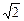 ,求
,求