题目内容
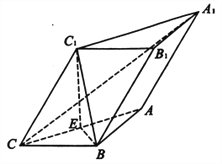
【题目】如图,在三棱柱![]() 中,平面
中,平面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,侧棱
的中点,侧棱![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析: (1)由![]() 和平面
和平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,可推得
,可推得![]() 平面
平面![]() ,进而推得
,进而推得![]() , 又
, 又![]() ,根据线面垂直的判定定理即可证得;(2)∵面
,根据线面垂直的判定定理即可证得;(2)∵面![]() 面
面![]() ,∴
,∴![]() 在面
在面![]() 上的射影
上的射影![]() 在
在![]() 上,∴
上,∴![]() 为直线
为直线![]() 与面
与面![]() 所成的角.求出CH和
所成的角.求出CH和![]() ,代入计算即可.
,代入计算即可.
试题解析:(1)证明:∵![]() ,
,![]() 为
为![]() 的中点,∴
的中点,∴![]() ,又平面
,又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() ,
,![]() ,∴
,∴![]() 面
面![]() .
.
(2)∵面![]() 面
面![]() ,∴
,∴![]() 在面
在面![]() 上的射影
上的射影![]() 在
在![]() 上,∴
上,∴![]() 为直线
为直线![]() 与面
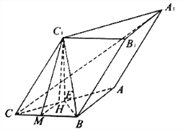
与面![]() 所成的角.过
所成的角.过![]() 作
作![]() 于
于![]() ,连
,连![]() ,
,
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() .
.
∴在![]() 中,
中,![]() .
.
∴直线![]() 与面
与面![]() 所成的角的余弦值为
所成的角的余弦值为![]()
点睛:本题考查的是线面垂直的判定定理的应用以及求线面角,属于中档题目. 判定直线和平面垂直的方法:①定义法.②利用判定定理:一条直线和一个平面内的两条相交直线都垂直,则该直线和此平面垂直.③推论:如果在两条平行直线中,有一条垂直于一个平面,那么另一条直线也垂直这个平面.

练习册系列答案
相关题目
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.