题目内容
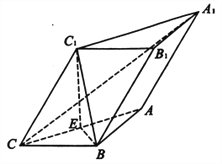
【题目】如图,直三棱柱 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上的动点.
上的动点.
证明: ![]() ;
;
若平面![]() 分该棱柱为体积相等的两个部分,试确定点
分该棱柱为体积相等的两个部分,试确定点![]() 的位置,并求二面角
的位置,并求二面角![]() 的大小.
的大小.

【答案】(1)见解析(2)30°
【解析】试题分析:(1)由![]() 平面
平面![]() 得
得![]() ,再由
,再由![]() ,得
,得![]() 平面
平面![]() ,
,
所以![]() ;(2)根据割补法求
;(2)根据割补法求![]() ,根据体积为三棱柱一半,求得
,根据体积为三棱柱一半,求得![]() 为
为![]() 中点;)取
中点;)取![]() 的中点
的中点![]() ,根据垂直关系可得
,根据垂直关系可得![]() 是二面角
是二面角![]() 的平面角.最后解三角形可得二面角
的平面角.最后解三角形可得二面角![]() 的大小
的大小
试题解析:解:(I)![]() 平面
平面![]() ,
, ![]()
又![]() ,即
,即![]()
![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
, ![]() ;
;
(II) ![]() ,
,
依题意![]() ,
,
![]() 为
为![]() 中点;
中点;
(法1)取![]() 的中点
的中点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]()
![]() ,面
,面![]() 面
面![]() 面
面![]()
![]() ,得点
,得点![]() 与点
与点![]() 重合,且
重合,且![]() 是二面角
是二面角![]() 的平面角.
的平面角.
设![]() ,则
,则![]() ,得二面角的大小为30°.
,得二面角的大小为30°.
(法2)以![]() 为空间坐标原点,
为空间坐标原点, ![]() 为
为![]() 轴正向、
轴正向、![]() 为
为![]() 轴正向、
轴正向、![]() 为
为![]() 轴正向,建立空间直角坐标系,设
轴正向,建立空间直角坐标系,设![]() 的长为 1,则
的长为 1,则![]() .
.
作![]() 中点
中点![]() ,连结
,连结![]() ,则
,则![]() ,从而
,从而![]() 平面
平面![]() ,平面
,平面![]() 的一个法向量
的一个法向量![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则![]()
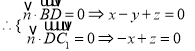 ,令
,令![]() ,得
,得![]() ,
, ![]()
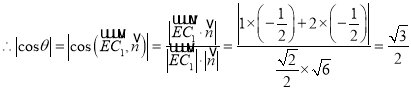
故二面角![]() 为30°.
为30°.

练习册系列答案
相关题目
【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关,通过随机抽查110名学生,得到如下2×2的列联表:
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式![]() ,算得
,算得![]()
附表:
| 0.025 | 0.01 | 0.005 |
| 5.024 | 6.635 | 7.879 |
参照附表,以下结论正确是( )
A. 有![]() 以上的把握认为“爱好该项运动与性别有关”
以上的把握认为“爱好该项运动与性别有关”
B. 有![]() 以上的把握认为“爱好该项运动与性别无关”
以上的把握认为“爱好该项运动与性别无关”
C. 有![]() 以上的把握认为“爱好该项运动与性别有关”
以上的把握认为“爱好该项运动与性别有关”
D. 有![]() 以上的把握认为“爱好该项运动与性别无关”
以上的把握认为“爱好该项运动与性别无关”