题目内容
8.设函数f(x)=ax-(k-1)a-x(a>0,且a≠1)是定义域为R的奇函数.(1)求k的值;
(2)若f(1)<0,试判断函数单调性,并求使不等式f(x2+tx)+f(4-x)<0恒成立的t的取值范围;
(3)若a=2,且g(x)=f2(x)-2mf(x)+2在[1,+∞)上的最小值为-2,求m的值.
分析 (1)根据奇函数的性质可得f(0)=0,由此求得k值;
(2)由f(x)=ax-a-x(a>0且a≠1),f(1)<0,求得0<a<1,f(x)在R上单调递减,不等式化为f(x2+tx)<f(x-4),即x2+(t-1)x+4>0 恒成立,
由△<0求得t的取值范围;
(3)把a=2代入函数f(x)的解析式,令t=f(x)=2x-2-x(x≥1)换元,求出t的范围,则y=g(x)=f2(x)-2mf(x)+2=t2-2mt+2,然后利用二次函数的单调性求得y的最小值,由最小值为-2求m的值.
解答 解:(1)∵f(x)是定义域为R的奇函数,∴f(0)=0,
∴1-(k-1)=0,∴k=2.
当k=2时,f(x)=ax-a-x(a>0且a≠1),∴f(-x)=-f(x)成立,
∴f(x)是定义域为R的奇函数;
(2)函数f(x)=ax-a-x(a>0且a≠1),
∵f(1)<0,∴a-$\frac{1}{a}$<0,
∵a>0,∴0<a<1.
由于y=ax单调递减,y=a-x单调递增,故f(x)在R上单调递减.
不等式f(x2+tx)+f(4-x)<0,可化为f(x2+tx)<f(x-4).
∴x2+tx>x-4,即x2+(t-1)x+4>0 恒成立,
∴△=(t-1)2-16<0,解得-3<t<5;
(3)a=2时,f(x)=2x-2-x,令t=f(x)=2x-2-x(x≥1),则t$≥\frac{3}{2}$.
∴y=g(x)=f2(x)-2mf(x)+2=t2-2mt+2.
对称轴方程为t=m,当m$≤\frac{3}{2}$时,y=t2-2mt+2在[$\frac{3}{2},+∞$)上为增函数,${y}_{min}=(\frac{3}{2})^{2}-2m•\frac{3}{2}+2=\frac{17}{4}-3m$,
由$\frac{17}{4}-3m=-2$,解得:m=$\frac{25}{12}$(舍);
当m$>\frac{3}{2}$时,y=t2-2mt+2在[$\frac{3}{2},m$)上为减函数,在(m,+∞)上为增函数,${y}_{min}={m}^{2}-2{m}^{2}+2=2-{m}^{2}$,
由2-m2=-2,解得m=-2(舍)或m=2.
∴m=2.
点评 本题考查指数型复合函数的性质以及应用,考查函数的奇偶性的应用,训练了利用二次函数的单调性求函数的最值,属于中高档题.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案| A. | eaf(a)>ebf(b) | B. | ebf(a)>eaf(b) | C. | ebf(b)>eaf(a) | D. | eaf(b)>ebf(a) |

| A. | $\frac{3}{4}$ | B. | 3 | C. | 4 | D. | 7 |
| x | 0 | 1 | 2 | 3 |
| y | 1 | 2 | 6 | 7 |
| A. | (1,3) | B. | (2,6) | C. | (3,7) | D. | (1.5,4) |
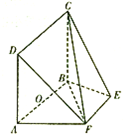 如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.
如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.