题目内容
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() ,解不等式
,解不等式![]() ;
;
(Ⅱ)若不等式![]() 至少有一个负数解,求实数
至少有一个负数解,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ){x|1≤x≤0}.(Ⅱ)(![]()
![]() ,2).
,2).
【解析】【试题分析】(I)当![]() 时,利用零点分段法去绝对值,将不等式变为分段不等式来求得解集.(II)作出函数
时,利用零点分段法去绝对值,将不等式变为分段不等式来求得解集.(II)作出函数![]() 的图象和函数
的图象和函数![]() 的图象,通过数形结合与分类讨论的数学思想方法求得
的图象,通过数形结合与分类讨论的数学思想方法求得![]() 的取值范围.
的取值范围.
【试题解析】
(Ⅰ)若a=1,则不等式![]() +
+![]() ≥3化为2
≥3化为2![]() +|x1|≥3.
+|x1|≥3.
当x≥1时,2![]() +x1≥3,即
+x1≥3,即![]() x+2≤0,(x
x+2≤0,(x![]()
![]() )2+
)2+![]()
![]() ≤0不成立;
≤0不成立;
当x<1时,2![]() x+1≥3,即
x+1≥3,即![]() +x≤0,解得1≤x≤0.
+x≤0,解得1≤x≤0.
综上,不等式![]() +
+![]() ≥3的解集为{x|1≤x≤0}.
≥3的解集为{x|1≤x≤0}.
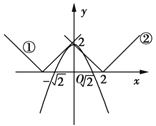
(Ⅱ)作出y=![]() 的图象如图所示,当a<0时,
的图象如图所示,当a<0时,![]() 的图象如折线①所示,
的图象如折线①所示,
由![]() ,
,![]() 得
得![]() +xa2=0,若相切,则Δ=1+4(a+2)=0,得a=
+xa2=0,若相切,则Δ=1+4(a+2)=0,得a=![]() ,
,
数形结合知,当a≤![]()
![]() 时,不等式无负数解,则
时,不等式无负数解,则![]()
![]() <a<0.
<a<0.
当a=0时,满足![]() >
>![]() 至少有一个负数解.
至少有一个负数解.
当a>0时,![]() 的图象如折线②所示,
的图象如折线②所示,
此时当a=2时恰好无负数解,数形结合知,
当a≥2时,不等式无负数解,则0<a<2.
综上所述,若不等式![]() >
>![]() 至少有一个负数解,
至少有一个负数解,
则实数a的取值范围是(![]()
![]() ,2).
,2).

【题目】某蛋糕店制作并销售一款蛋糕,当天每售出![]() 个利润为
个利润为![]() 元,未售出的每个亏损
元,未售出的每个亏损![]() 元.根据以往
元.根据以往![]() 天的统计资料,得到如下需求量表,元旦这天,此蛋糕店制作了
天的统计资料,得到如下需求量表,元旦这天,此蛋糕店制作了![]() 个这种蛋糕.以
个这种蛋糕.以![]() (单位:个,
(单位:个, ![]() )表示这天的市场需求量.
)表示这天的市场需求量. ![]() (单位:元)表示这天售出该蛋糕的利润.
(单位:元)表示这天售出该蛋糕的利润.
需求量/个 |
|
|
|
|
|
天数 | 10 | 20 | 30 | 25 | 15 |
(1)将![]() 表示为
表示为![]() 的函数,根据上表,求利润
的函数,根据上表,求利润![]() 不少于
不少于![]() 元的概率;
元的概率;
![]() 天的平均需求量(同一组数据用该区间的中点值作代表);
天的平均需求量(同一组数据用该区间的中点值作代表);
(3)元旦这天,该店通过微信展示打分的方式随机抽取了![]() 名市民进行问卷调查,调查结果如下表所示,已知在购买意愿强的市民中,女性的占比为
名市民进行问卷调查,调查结果如下表所示,已知在购买意愿强的市民中,女性的占比为![]() .
.
购买意愿强 | 购买意愿弱 | 合计 | |
女性 | 28 | ||
男性 | 22 | ||
合计 | 28 | 22 | 50 |
完善上表,并根据上表,判断是否有![]() 的把握认为市民是否购买这种蛋糕与性别有关?
的把握认为市民是否购买这种蛋糕与性别有关?
附:  .
.
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |


