题目内容
【题目】已知函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() ,存在
,存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析 (2) ![]() .
.
【解析】
(1)根据![]() 的不同取值,结合绝对值的性质,分类讨论求出函数
的不同取值,结合绝对值的性质,分类讨论求出函数![]() 的单调区间;
的单调区间;
(2) 求出二次函数的对称轴,根据对称轴和所给的区间的位置进行分类讨论,即可求出实数![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时, ![]() ,因此函数在
,因此函数在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,
时, 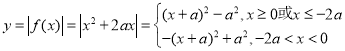 ,
,
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减;
上单调递减;
当![]() 时,
时, 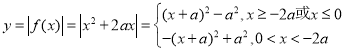 ,
,
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减;
上单调递减;
(2)二次函数的对称轴为:![]() .
.
①当![]() 时,二次函数
时,二次函数![]() 是单调减函数,因此有:
是单调减函数,因此有:
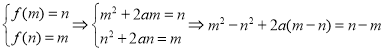
![]()
![]() ,
,
所以一元二次方程![]() 在区间
在区间![]() 上有两不等根,则有
上有两不等根,则有

![]() ;
;
②当![]() 时,二次函数
时,二次函数![]() 是单调增函数,因此有:
是单调增函数,因此有:
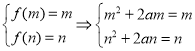 ,所以
,所以![]() 可以看成一元二次方程
可以看成一元二次方程![]() 两根,则
两根,则![]() ,有
,有![]() ;
;
③当![]() 时,
时, ![]() ,所以由
,所以由![]()
函数的最大值是![]() 中的一个值,
中的一个值, ![]() .
.
①若![]() 时,有
时,有![]() ,此时
,此时![]() ,所以
,所以![]() 或
或![]()
(i)若![]() 时,
时, ![]()
(ii)若![]() ,由
,由![]() (舍):
(舍):
②若![]() 时,有
时,有![]() ,此时
,此时![]() ,
,
因此有![]() ,
,
根据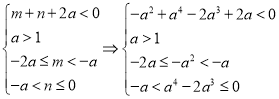
![]()
综上所述:实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】某商场按月订购一种家用电暖气,每销售一台获利润200元,未销售的产品返回厂家,每台亏损50元,根据往年的经验,每天的需求量与当天的最低气温有关,如果最低气温位于区间![]() ,需求量为100台;最低气温位于区间
,需求量为100台;最低气温位于区间![]() ,需求量为200台;最低气温位于区间
,需求量为200台;最低气温位于区间![]() ,需求量为300台。公司销售部为了确定11月份的订购计划,统计了前三年11月份各天的最低气温数据,得到下面的频数分布表:
,需求量为300台。公司销售部为了确定11月份的订购计划,统计了前三年11月份各天的最低气温数据,得到下面的频数分布表:
最低气温(℃) |
|
|
|
|
|
天数 | 11 | 25 | 36 | 16 | 2 |
以最低气温位于各区间的频率代替最低气温位于该区间的概率.
求11月份这种电暖气每日需求量![]() (单位:台)的分布列;
(单位:台)的分布列;
若公司销售部以每日销售利润![]() (单位:元)的数学期望为决策依据,计划11月份每日订购200台或250台,两者之中选其一,应选哪个?
(单位:元)的数学期望为决策依据,计划11月份每日订购200台或250台,两者之中选其一,应选哪个?

