题目内容
【题目】如图,已知在四棱锥![]() 中,
中,![]() 平面
平面![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() ,底面为直角梯形,
,底面为直角梯形,![]()
![]()
![]() 分别是
分别是![]() 的中点.
的中点.

(1)求证:![]() //平面
//平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见证明;(2) ![]() (3)
(3)![]()
【解析】
(1)法一:构造平行四边形,利用三角形中位线定理,证明平行,即可.法二:建立空间坐标系,计算各点坐标,计算平面PBC的法向量,结合向量数量积公式,即可.(2)利用向量数量积公式,代入坐标,即可.(3)结合向量数量积公式,代入,即可.
(1)法一:![]() ,则
,则![]() //
//![]() ,
,![]()
依题意得,![]() //
//![]() ,
,![]() ,
,
所以![]() 为平行四边形,
为平行四边形,
![]() //
//![]()
![]()
又![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() , ∴
, ∴![]() //平面
//平面![]()
法二:以![]() 为原点,以
为原点,以![]() 分别为
分别为![]() 建立空间直角坐标系
建立空间直角坐标系![]() ,
,
由![]()
![]() ,
,![]() 分别是
分别是![]() 的中点,可得:
的中点,可得:
![]()
![]()

∴![]() ,
,![]()
设平面的![]() 的法向量为
的法向量为![]() ,
,
则有:
令![]() ,则
,则![]() ,
,
∴![]() ,又
,又![]() 平面
平面![]()
∴![]() //平面
//平面![]()
(2)设平面的![]() 的法向量为
的法向量为![]() ,
,
又![]()
则有: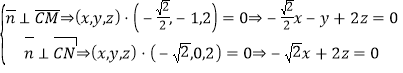
令![]() ,则
,则![]() ,
,
又![]() ,
,
∴ ,
,
∴求直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]()
(3)![]()
∴点![]() 到平面
到平面![]() 的距离
的距离![]() .
.

【题目】某商场按月订购一种家用电暖气,每销售一台获利润200元,未销售的产品返回厂家,每台亏损50元,根据往年的经验,每天的需求量与当天的最低气温有关,如果最低气温位于区间![]() ,需求量为100台;最低气温位于区间
,需求量为100台;最低气温位于区间![]() ,需求量为200台;最低气温位于区间
,需求量为200台;最低气温位于区间![]() ,需求量为300台。公司销售部为了确定11月份的订购计划,统计了前三年11月份各天的最低气温数据,得到下面的频数分布表:
,需求量为300台。公司销售部为了确定11月份的订购计划,统计了前三年11月份各天的最低气温数据,得到下面的频数分布表:
最低气温(℃) |
|
|
|
|
|
天数 | 11 | 25 | 36 | 16 | 2 |
以最低气温位于各区间的频率代替最低气温位于该区间的概率.
求11月份这种电暖气每日需求量![]() (单位:台)的分布列;
(单位:台)的分布列;
若公司销售部以每日销售利润![]() (单位:元)的数学期望为决策依据,计划11月份每日订购200台或250台,两者之中选其一,应选哪个?
(单位:元)的数学期望为决策依据,计划11月份每日订购200台或250台,两者之中选其一,应选哪个?
【题目】已知![]() 三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
| 6 |
| 7 | |
| 6 | 7 | 8 | |
| 5 | 6 | 7 | 8 |
(Ⅰ)试估计![]() 班学生人数;
班学生人数;
(Ⅱ)从![]() 班和
班和![]() 班抽出来的学生中各选一名,记
班抽出来的学生中各选一名,记![]() 班选出的学生为甲,
班选出的学生为甲,![]() 班选出的学生为乙,若学生锻炼相互独立,求甲的锻炼时间大于乙的锻炼时间的概率.
班选出的学生为乙,若学生锻炼相互独立,求甲的锻炼时间大于乙的锻炼时间的概率.