题目内容
【题目】如图,三角形![]() 中,
中,![]() ,
,![]() 是边长为l的正方形,平面
是边长为l的正方形,平面![]() 底面
底面![]() ,若
,若![]() 分别是
分别是![]() 的中点.
的中点.
(1)求证:![]() 底面
底面![]() ;
;
(2)求几何体![]() 的体积.
的体积.

【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)通过面面平行证明线面平行,所以取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() .只需通过证明HG//BC,HF//AB来证明面GHF//面ABC,从而证明
.只需通过证明HG//BC,HF//AB来证明面GHF//面ABC,从而证明![]() 底面
底面![]() 。
。
(2)原图形可以看作是以点C为顶点,ABDE为底的四棱锥,所四棱锥的体积公式可求得体积。
试题解析:(1)取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() .(如图)
.(如图)
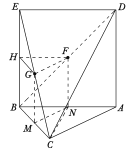
∵![]() 分别是
分别是![]() 和
和![]() 的中点,
的中点,
∴![]() ,且
,且![]() ,
,
![]() ,且
,且![]() .
.
又∵![]() 为正方形,∴
为正方形,∴![]() ,
,![]() .
.
∴![]() 且
且![]() .
.
∴![]() 为平行四边形.
为平行四边形.
∴![]() ,又
,又![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)因为![]() ,∴
,∴![]() ,
,
又平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
∵三角形![]() 是等腰直角三角形,∴
是等腰直角三角形,∴![]() .
.
∵![]() 是四棱锥,
是四棱锥,
∴![]()
![]() .
.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目

