题目内容
如图,南北方向的公路 ,A地在公路正东2 km处,B地在A东偏北300方向2
,A地在公路正东2 km处,B地在A东偏北300方向2 km处,河流沿岸曲线
km处,河流沿岸曲线 上任意一点到公路
上任意一点到公路 和到
和到 地距离相等.现要在曲线
地距离相等.现要在曲线 上一处建一座码头,向
上一处建一座码头,向 两地运货物,经测算,从
两地运货物,经测算,从 到
到 、到
、到 修建费用都为a万元/km,那么,修建这条公路的总费用最低是( )万元
修建费用都为a万元/km,那么,修建这条公路的总费用最低是( )万元
A.(2+ )a )a | B.2( +1)a +1)a | C.5a | D.6ª |
C
解析试题分析:解:依题意知曲线PQ是以A为焦点、l为准线的抛物线的一支,根据抛物线的定义知:欲求从M到A,B修建公路的费用最低,只须求出B到直线l距离即可.因B地在A地北偏东60°方向2 km处,∴B到点A的水平距离为:3,∴B到直线l距离为:3+2=5,那么修建这两条公路的总费用最低为:5a.故选C.
km处,∴B到点A的水平距离为:3,∴B到直线l距离为:3+2=5,那么修建这两条公路的总费用最低为:5a.故选C.
考点:抛物线的定义
点评:考查学生根据实际问题选择函数类型的能力,以及会用抛物线的定义的方法来求函数的最小值的能力.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
椭圆 上有两个动点
上有两个动点 、
、 ,
, ,
, ,则
,则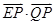 的最小值为( )
的最小值为( )
| A.6 | B. | C.9 | D. |
一个顶点的坐标 ,焦距的一半为3的椭圆的标准方程是( )
,焦距的一半为3的椭圆的标准方程是( )
A. | B. | C. | D. |
已知实数 ,
, ,
, 构成一个等比数列,则圆锥曲线
构成一个等比数列,则圆锥曲线 的离心率为( )
的离心率为( )
A. | B. | C. | D.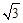 |
(5分)抛物线y2=4x的焦点到双曲线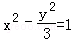 的渐近线的距离是( )
的渐近线的距离是( )
A. | B.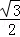 | C.1 | D.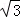 |
已知中心在原点的椭圆C的右焦点为 ,离心率等于
,离心率等于 ,则C的方程是( )
,则C的方程是( )
A. | B. | C. | D. |
 的焦点
的焦点 与椭圆
与椭圆 的一个焦点重合,它们在第一象限内的交点为
的一个焦点重合,它们在第一象限内的交点为 ,且
,且 与
与 轴垂直,则椭圆的离心率为( )
轴垂直,则椭圆的离心率为( )



 的两个焦点分别为
的两个焦点分别为 、
、 ,若曲线
,若曲线 满足
满足 :
: :
: =4:3:2,则曲线
=4:3:2,则曲线