题目内容
设圆锥曲线 的两个焦点分别为
的两个焦点分别为 、
、 ,若曲线
,若曲线 上存在点
上存在点 满足
满足 :
: :
: =4:3:2,则曲线
=4:3:2,则曲线 的离心率等于( )
的离心率等于( )
A. | B. | C. | D.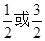 |
D
解析试题分析:根据题意,该圆锥曲线可能是椭圆,也可能是双曲线,那么当为前者时,则有点 满足
满足 :
: :
: =4:3:2,由椭圆定义可知,2a=6,2c=3则离心率为
=4:3:2,由椭圆定义可知,2a=6,2c=3则离心率为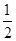 ,当当为后者时,则有点
,当当为后者时,则有点 满足
满足 :
: :
: =4:3:2,由双曲线定义可知,2a=2,2c=3则离心率为
=4:3:2,由双曲线定义可知,2a=2,2c=3则离心率为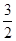 ,故可知结论为
,故可知结论为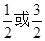 ,选D
,选D
考点:圆锥曲线的性质
点评:主要是考查了圆锥曲线的共同的性质的运用,属于基础题。

练习册系列答案
相关题目
双曲线 的渐近线方程是( )
的渐近线方程是( )
A. | B. | C. | D. |
椭圆 的离心率为 ( )
的离心率为 ( )
A. | B. | C. | D. |
如图,南北方向的公路 ,A地在公路正东2 km处,B地在A东偏北300方向2
,A地在公路正东2 km处,B地在A东偏北300方向2 km处,河流沿岸曲线
km处,河流沿岸曲线 上任意一点到公路
上任意一点到公路 和到
和到 地距离相等.现要在曲线
地距离相等.现要在曲线 上一处建一座码头,向
上一处建一座码头,向 两地运货物,经测算,从
两地运货物,经测算,从 到
到 、到
、到 修建费用都为a万元/km,那么,修建这条公路的总费用最低是( )万元
修建费用都为a万元/km,那么,修建这条公路的总费用最低是( )万元
A.(2+ )a )a | B.2( +1)a +1)a | C.5a | D.6ª |
已知点A(1,0)和圆 上一点P,动点Q满足
上一点P,动点Q满足 ,则点Q的轨迹方程为( )
,则点Q的轨迹方程为( )
A. | B. |
C. | D. |
若P是双曲线 :
: 和圆
和圆 :
: 的一个交点且
的一个交点且
 ,其中
,其中 是双曲线
是双曲线 的两个焦点,则双曲线
的两个焦点,则双曲线 的离心率为
的离心率为
A. | B. | C.2 | D.3 |
 的离心率为
的离心率为
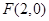 是右焦点.若
是右焦点.若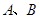 为双曲线上关于原点对称的两点,且
为双曲线上关于原点对称的两点,且 ,则直线
,则直线 的斜率是( )
的斜率是( )



 围成的区域(含边界)为Ωn(n=1,2,…),当点(x,y)分别在Ω1,Ω2,…上时,x+y的最大值分别是M1,M2,…,则
围成的区域(含边界)为Ωn(n=1,2,…),当点(x,y)分别在Ω1,Ω2,…上时,x+y的最大值分别是M1,M2,…,则 Mn=( )
Mn=( )

 ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线 的焦点重合, 则此椭圆方程为
的焦点重合, 则此椭圆方程为


