题目内容
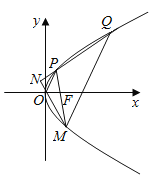
【题目】如图,已知椭圆![]() ,
,![]() 分别为其左、右焦点,过
分别为其左、右焦点,过![]() 的直线与此椭圆相交于
的直线与此椭圆相交于![]() 两点,且
两点,且![]() 的周长为8,椭圆
的周长为8,椭圆![]() 的离心率为
的离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在平面直角坐标系![]() 中,已知点
中,已知点![]() 与点
与点![]() ,过
,过![]() 的动直线
的动直线![]() (不与
(不与![]() 轴平行)与椭圆相交于
轴平行)与椭圆相交于![]() 两点,点
两点,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点.求证:
轴的对称点.求证:
(i)![]() 三点共线.
三点共线.
(ii)![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
![]() Ⅰ
Ⅰ![]() 由三角形的周长可得
由三角形的周长可得![]() ,根据离心率可得
,根据离心率可得![]() ,即可求出
,即可求出![]() ,则椭圆方程可求;
,则椭圆方程可求;![]() Ⅱ
Ⅱ![]() 当直线l的斜率不存在时,A、B分别为椭圆短轴两端点,满足Q,A,
当直线l的斜率不存在时,A、B分别为椭圆短轴两端点,满足Q,A,![]() 三点共线
三点共线![]() 当直线l的斜率存在时,设直线方程为
当直线l的斜率存在时,设直线方程为![]() ,联立直线方程与椭圆方程,化为关于x的一元二次方程,然后利用向量证明.
,联立直线方程与椭圆方程,化为关于x的一元二次方程,然后利用向量证明.![]() 由
由![]() 可知Q,A,
可知Q,A,![]() 三点共线,即
三点共线,即![]() ,问题得以证明.
,问题得以证明.
解:![]() Ⅰ
Ⅰ![]() 的周长为8,
的周长为8,![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
故椭圆C的方程为![]()
![]() Ⅱ
Ⅱ![]() 证明:当直线l的斜率不存在时,A、B分别为椭圆短轴两端点,满足Q,A,
证明:当直线l的斜率不存在时,A、B分别为椭圆短轴两端点,满足Q,A,![]() 三点共线.
三点共线.
当直线l的斜率存在时,设直线方程为![]() ,
,
联立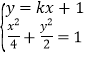 ,得
,得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() .
.
![]() 与
与![]() 共线,则Q,A,
共线,则Q,A,![]() 三点共线.
三点共线.
![]() 由
由![]() 可知Q,A,
可知Q,A,![]() 三点共线,
三点共线,
![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目