题目内容
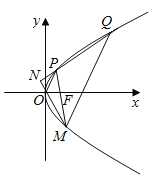
【题目】设F是抛物线y2=4x的焦点,M,P,Q是抛物线上三个不同的动点,直线PM过点F,MQ∥OP,直线QP与MO交于点N.记点M,P,Q的纵坐标分别为y0,y1,y2.
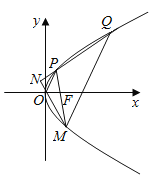
(1)证明:y0=y1﹣y2;
(2)证明:点N的横坐标为定值.
【答案】(1)证明见解析 (2) 证明见解析
【解析】
(1) 由两直线平行的条件:斜率相等,运用直线的斜率公式,结合点在抛物线上,化简可得结论(2) 因为直线![]() 过点
过点![]() ,所以
,所以![]() ,求得直线
,求得直线![]() ,
,![]() 的方程,设点
的方程,设点![]() 坐标为
坐标为![]() ,又因为直线
,又因为直线![]() ,
,![]() 交于点
交于点![]() ,化简整理可得
,化简整理可得![]() ,
,![]() 的方程,分解因式即可得到定值.
的方程,分解因式即可得到定值.
证明:(1) 因为MQ∥OP,所以kMQ=kOP,
所以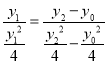 ,所以y0=y1﹣y2;
,所以y0=y1﹣y2;
(2) 因为直线PM过点F,
可得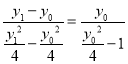 ,
,
所以y1y0=﹣4,
由(1)得y0=y1﹣y2,所以y1![]() ,y2
,y2![]() y0,
y0,
因为OM:y![]() x,
x,
PQ:y﹣y1![]() (x
(x![]() ),
),
即4x﹣(y1+y2)y+y1y2=0,
设点N坐标为(m,n),又因为直线QP,MO交于点N,
所以n![]() m,4m﹣(y1+y2)n+y1y2=0,
m,4m﹣(y1+y2)n+y1y2=0,
可得y0![]() ,4m﹣(
,4m﹣(![]() y0)n+(
y0)n+(![]() )(
)(![]() y0)=0,
y0)=0,
消去y0得2mn2+n2+8m3+4m2=0,
所以(2m+1)n2+4m2(2m+1)=0,
所以(2m+1)(n2+4m2)=0,
因为n2+4m2≠0,
所以2m+1=0,即m![]() ,
,
所以点N的横坐标为定值![]() .
.

练习册系列答案
相关题目