题目内容
(本小题满分12分)标准椭圆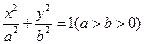 的两焦点为
的两焦点为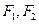 ,
,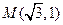 在椭圆上,且
在椭圆上,且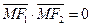 . (1)求椭圆方程;(2)若N在椭圆上,O为原点,直线
. (1)求椭圆方程;(2)若N在椭圆上,O为原点,直线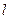 的方向向量为
的方向向量为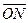 ,若
,若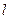 交椭圆于A、B两点,且NA、NB与
交椭圆于A、B两点,且NA、NB与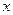 轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB),则称N点为椭圆的特征点,求该椭圆的特征点.
轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB),则称N点为椭圆的特征点,求该椭圆的特征点.
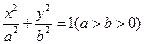 的两焦点为
的两焦点为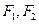 ,
,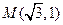 在椭圆上,且
在椭圆上,且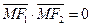 . (1)求椭圆方程;(2)若N在椭圆上,O为原点,直线
. (1)求椭圆方程;(2)若N在椭圆上,O为原点,直线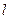 的方向向量为
的方向向量为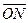 ,若
,若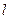 交椭圆于A、B两点,且NA、NB与
交椭圆于A、B两点,且NA、NB与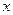 轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB),则称N点为椭圆的特征点,求该椭圆的特征点.
轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB),则称N点为椭圆的特征点,求该椭圆的特征点.(Ⅰ) 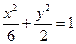 (Ⅱ)
(Ⅱ) 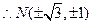
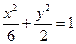 (Ⅱ)
(Ⅱ) 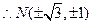
(1)在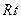
 中,
中,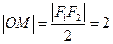 知
知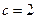
 则
则 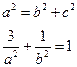 解得
解得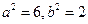
 椭圆方程为
椭圆方程为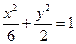 ………4分
………4分
(2)设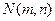 (m≠0),
(m≠0),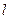 为
为 ,
,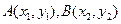
由 与
与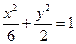 得
得 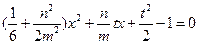 ………6分
………6分
由点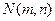 在椭圆上知,
在椭圆上知,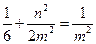 代入得
代入得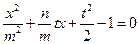
∴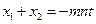
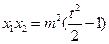 ,① …………8分
,① …………8分
∴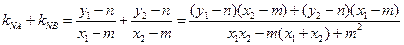
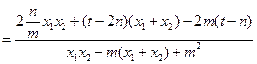 将①式代入得
将①式代入得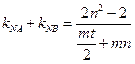
又∵NA、NB与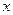 轴围成的三角形是等腰三角形得
轴围成的三角形是等腰三角形得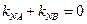 ,…………10分
,…………10分
∴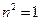 代入
代入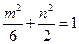 得
得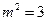
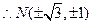 …12分
…12分
 中,
中,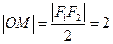 知
知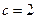
 则
则 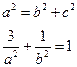 解得
解得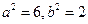
 椭圆方程为
椭圆方程为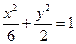 ………4分
………4分(2)设
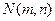 (m≠0),
(m≠0),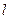 为
为 ,
,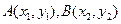
由
 与
与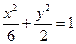 得
得 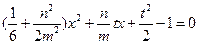 ………6分
………6分由点
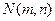 在椭圆上知,
在椭圆上知,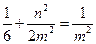 代入得
代入得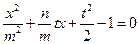
∴
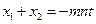
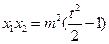 ,① …………8分
,① …………8分∴
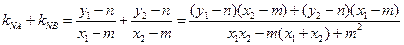
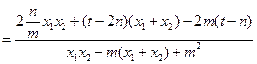 将①式代入得
将①式代入得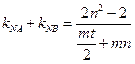
又∵NA、NB与
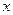 轴围成的三角形是等腰三角形得
轴围成的三角形是等腰三角形得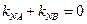 ,…………10分
,…………10分∴
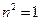 代入
代入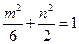 得
得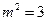
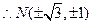 …12分
…12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
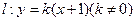 与椭圆
与椭圆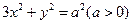 相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.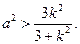 ;
;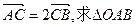 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.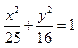 上一点,左、右焦点分别为F1,F2。
上一点,左、右焦点分别为F1,F2。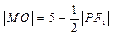
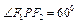 ,求
,求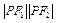 之值。
之值。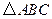 的顶点
的顶点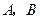 在椭圆
在椭圆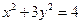 上,
上, 在直线
在直线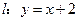 上,
上,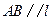 .
.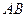 中点的轨迹方程;
中点的轨迹方程;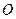 时,求
时,求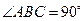 ,且斜边
,且斜边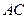 的长最大时,求
的长最大时,求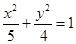 左焦点是
左焦点是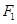 ,右焦点是
,右焦点是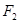 ,右准线是
,右准线是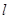 ,
,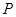 是
是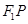 与椭圆交于点
与椭圆交于点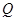 ,满足
,满足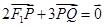 ,则
,则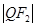 等于( )
等于( )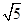


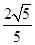
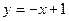 与椭圆
与椭圆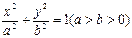 相交于A、B两点,且线段AB的中点,在直线
相交于A、B两点,且线段AB的中点,在直线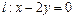 上.(1)求此椭圆的离心率;(2)若椭圆的右焦点关于直线
上.(1)求此椭圆的离心率;(2)若椭圆的右焦点关于直线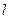 的对称点的在圆
的对称点的在圆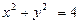 上,求此椭圆的方程.
上,求此椭圆的方程. 截圆柱体,截口是一条封闭曲线,且截面与底面所成的
截圆柱体,截口是一条封闭曲线,且截面与底面所成的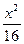 +
+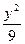 =1的两焦点,经点F2的的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( )
=1的两焦点,经点F2的的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( ) -
- =1表示焦点在y轴上的椭圆,那么实数a的取值范围是…( )
=1表示焦点在y轴上的椭圆,那么实数a的取值范围是…( )