题目内容
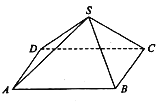
【题目】如图,已知四棱锥中,四边形![]() 为矩形,
为矩形,![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)设![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的二面角的正弦值.
所成的二面角的正弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)证明BC![]() 平面SDC,即可证得AD
平面SDC,即可证得AD![]() 平面SDC,即可证得SC
平面SDC,即可证得SC![]() AD,利用SC2+SD2=DC2证得SC
AD,利用SC2+SD2=DC2证得SC![]() SD,问题得证。
SD,问题得证。
(2)以点O为原点,建立坐标系如图,求得S(0,0,![]() ),C(0,
),C(0,![]() ,0), A(2,-
,0), A(2,-![]() ,0),B(2,
,0),B(2,![]() ,0),利用
,0),利用![]() 即可求得E(2,
即可求得E(2,![]() ,0),求得
,0),求得![]()
![]() ,
,![]()
![]() ,利用空间向量夹角公式计算即可得解。
,利用空间向量夹角公式计算即可得解。
(1)证明: BC![]() SD ,BC
SD ,BC![]() CD
CD
则BC![]() 平面SDC, 又
平面SDC, 又![]()
则AD![]() 平面SDC,
平面SDC,![]() 平面SDC
平面SDC
SC![]() AD
AD
又在△SDC中,SC=SD=2, DC=AB![]() ,故SC2+SD2=DC2
,故SC2+SD2=DC2
则SC![]() SD ,又
SD ,又![]()
所以 SC![]() 平面SAD
平面SAD
(2)解:作SO![]() CD于O,因为BC
CD于O,因为BC![]() 平面SDC,
平面SDC,
所以平面ABCD![]() 平面SDC,故SO
平面SDC,故SO![]() 平面ABCD
平面ABCD
以点O为原点,建立坐标系如图.
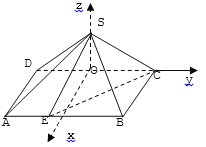
则S(0,0,![]() ),C(0,
),C(0,![]() ,0), A(2,-
,0), A(2,-![]() ,0),B(2,
,0),B(2,![]() ,0)
,0)
设E(2,y,0),因为![]()
所以![]() 即E((2,
即E((2,![]() ,0)
,0)
![]()
![]()
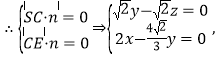 令
令![]() ,则
,则![]() ,
,![]()
![]()
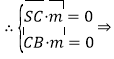
![]() ,令
,令![]() ,则
,则![]() ,
,![]()
![]()
![]()
所以所求二面角的正弦值为![]()

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目