题目内容
【题目】已知函数![]() (
(![]() 为常数).
为常数).
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,设
时,设![]() 的两个极值点
的两个极值点![]() ,(
,(![]() )恰为
)恰为![]() 的零点,求
的零点,求![]() 的最小值.
的最小值.
【答案】(Ⅰ)当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,当
,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题(1)先求函数导数![]() ,讨论导函数符号变化规律:当
,讨论导函数符号变化规律:当![]() 时,导函数不变号,故
时,导函数不变号,故![]() 的单调递增区间为
的单调递增区间为![]() .当
.当![]() 时,导函数符号由正变负,即单调递增区间为
时,导函数符号由正变负,即单调递增区间为![]() ,单调递减区间减区间为
,单调递减区间减区间为![]() ,(2)先求
,(2)先求![]() 导数得
导数得![]() 为方程
为方程![]() 的两根,再求
的两根,再求![]() 导数得
导数得![]() ,因此
,因此![]() ,而由
,而由![]() 为
为![]() 的零点,得
的零点,得![]() ,两式相减得
,两式相减得![]() ,即得
,即得![]() ,因此
,因此![]() ,从而
,从而![]()
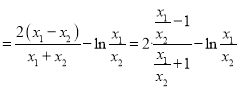
![]() ,其中
,其中![]() 根据韦达定理确定自变量范围:因为
根据韦达定理确定自变量范围:因为![]()
又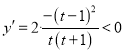 ,所以
,所以![]()
试题解析:(1)![]() ,当
,当![]() 时,由
时,由![]() 解得
解得![]() ,即当
,即当![]() 时,
时,![]() 单调递增, 由
单调递增, 由![]() 解得
解得![]() ,即当
,即当![]() 时,
时,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时,
时,![]() 故
故![]() ,即
,即![]() 在
在![]() 上单调递增,所以当
上单调递增,所以当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间减区间为
,单调递减区间减区间为![]() ,当
,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)![]() ,则
,则![]() ,所以
,所以![]() 的两根
的两根![]() 即为方程
即为方程![]() 的两根. 因为
的两根. 因为![]() ,所以
,所以![]() ,又因为
,又因为![]() 为
为![]() 的零点,所以
的零点,所以![]() ,两式相减得
,两式相减得![]() ,得
,得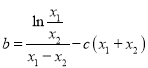 ,而
,而![]() ,
,
所以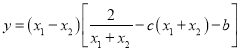
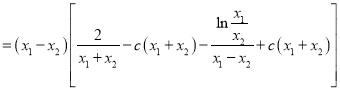
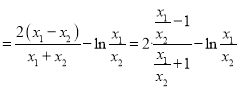
令![]() ,由
,由![]() 得
得![]()
因为![]() ,两边同时除以
,两边同时除以![]() ,得
,得![]() ,因为
,因为![]() ,故
,故![]() ,解得
,解得![]() 或
或![]() ,所以
,所以![]() ,设
,设![]() ,所以
,所以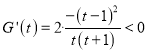 ,则
,则![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() ,即
,即![]() 的最小值为
的最小值为![]() .
.

【题目】某手机生产企业为了解消费者对某款手机的认同情况,通过销售部随机抽取50名购买该款手机的消费者,并发出问卷调查(满分50分),该问卷只有20份给予回复,这20份的评分如下:
男 | 47,36,28,48,48,44,50,46,50,37,35,49 |
女 | 38,37,50,36,38,45,29,39 |
(1)完成下面的茎叶图,并求12名男消费者评分的中位数与8名女消费者评分的众数及平均值;
男 | 女 | |
2 | ||
3 | ||
4 | ||
5 |
满意 | 不满意 | 合计 | |
男 | |||
女 | |||
合计 |
(2)若大于40分为“满意”,否则为“不满意”,完成上面的![]() 列联表,并判断是否有95%的把握认为消费者对该款手机的“满意度”与性别有关;
列联表,并判断是否有95%的把握认为消费者对该款手机的“满意度”与性别有关;
(3)若从回复的20名消费者中按性别用分层抽样的方法抽取5人,再从这5人中随机抽取2人作进一步调查,求至少有1名女性消费者被抽到的概率.
附:
| 0.05 | 0.025 | 0.01 |
| 3.841 | 5.024 | 6.635 |
【题目】某公司的新能源产品上市后在国内外同时销售,已知第一批产品上市销售40天内全部售完,该公司对这批产品上市后的国内外市场销售情况进行了跟踪调查,如图所示,其中图①中的折线表示的是国外市场的日销售量与上市时间的关系;图②中的抛物线表示的是国内市场的日销售量与上市时间的关系;下表表示的是产品广告费用、产品成本、产品销售价格与上市时间的关系.
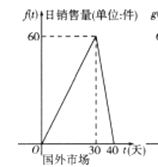 图① 图②
图① 图②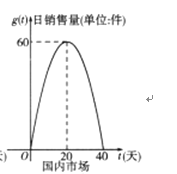
第t天产品广告费用(单位:万元) | 每件产品成本(单位:万元) | 每件产品销售价格(单位:万元) | |
|
| 3 | 6 |
| 10 | 3 | 5 |
(1)分别写出国外市场的日销售量![]() 、国内市场的日销售量
、国内市场的日销售量![]() 与产品上市时间t的函数关系式;
与产品上市时间t的函数关系式;
(2)产品上市后的哪几天,这家公司的日销售利润超过260万元?
(日销售利润=(单件产品销售价-单件产品成本)×日销售量-当天广告费用,![]() )
)