题目内容
【题目】某校组织的一次教师招聘共分笔试和面试两个环节，笔试环节共有20名大学毕业生参加，其中男、女生的比例恰好为
，其成绩的茎叶图如图所示.假设成绩在90分以上的考生可以进入面试环节.
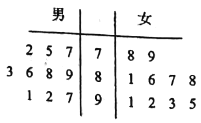
（1）试比较男、女两组成绩平均分的大小，并求出女生组的方差；
（2）从男、女两组可以进入面试环节的考生中分别任取1人，求两人分差不小于3分的概率.
【答案】（1）见解析；（2）
【解析】
（1）平均成绩等于各数据之和除以总人数，代入计算比较即可，根据方差的公式代入计算即可；
（2）一一列举满足：男、女两组可以进入面试环节的考生中分别任取1人的基本事件，然后找到满足：两人分差不小于3分的基本事件，利用古典概型计算即可．
（1）男生组的平均分为
；
女生组的平均分为
所以男生组的平均分低于女生组的平均分.
女生组的方差为：
（2）抽取情况为：91，91； 91，92； 91，93； 91，95；92，91； 92，92； 92，93； 92，95； 97，91； 97，92； 97，93； 97，95．总共有12种．
其中分差不小于3分的情况为91，95；92,95；97,91；97,92；97,93共5种．
所以所抽取的两人中，分差不小于3分的概率为.
应用题作业本系列答案
【题目】学校从参加高二年级期末考试的学生中抽出一些学生，并统计了他们的数学成绩（成绩均为整数且满分为100分），所得数据整理后，列出了如下频率分布表．
分组 | 频数 | 频率 |
[40，50） | A | 0.04 |
[50，60） | 4 | 0.08 |
[60，70） | 20 | 0.40 |
[70，80） | 15 | 0.30 |
[80，90） | 7 | B |
[90，100] | 2 | 0.04 |
合计 | C | 1 |
（1）在给出的样本频率分布表中，求A，B，C的值；
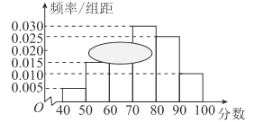
（2）补全频率分布直方图，并利用它估计全体高二年级学生期末数学成绩的众数、中位数；
（3）现从分数在[80，90），[90，100]的9名同学中随机抽取两名同学，求被抽取的两名学生分数均不低于90分的概率．