题目内容
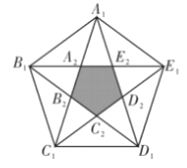
【题目】如图，用四种不同颜色给图中的A,B,C,D,E,F六个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同颜色，则不同的涂色方法用
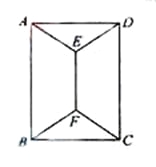
A.288种B.264种C.240种D.168种
【答案】B
【解析】
先分步再排列
先涂点E，有4种涂法，再涂点B，有两种可能：
(1)B与E相同时，依次涂点F，C，D，A，涂法分别有3，2，2，2种；
(2)B与E不相同时有3种涂法，再依次涂F、C、D、A点，涂F有2种涂法，涂C点时又有两种可能：
（2.1）C与E相同，有1种涂法，再涂点D，有两种可能：
①D与B相同，有1种涂法，最后涂A有2种涂法；
②D与B不相同，有2种涂法，最后涂A有1种涂法．
（2.2）C与E不相同，有1种涂法，再涂点D，有两种可能：
①D与B相同，有1种涂法，最后涂A有2种涂法；
②D与B不相同，有2种涂法，最后涂A有1种涂法．
所以不同的涂色方法有
4×{3×2×2×2+3×2×[1×(1×2+1×2)+1×(1×2+1×1)]}=4×(24+42)=264．
练习册系列答案
教学练新同步练习系列答案
相关题目
