题目内容
11．
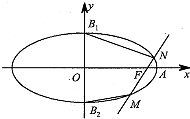已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0），其右顶点为 A（2，0），上、下顶点分别为 B1，B2．直线 A B2的斜率为$\frac{1}{2}$，过椭圆的右焦点F的直线交椭圆于 M，N两点（ M，N均在y轴右侧）．（Ⅰ）求椭圆的方程；
（Ⅱ）设四边形 M N B1 B2面积为S，求S的取值范围．
分析 （Ⅰ）因为a=2，$\frac{b}{a}=\frac{1}{2}$，所以b=1，可求得椭圆方程
（Ⅱ）设M（x1，y1）N（x2，y2），直线MN方程为x=my+$\sqrt{3}$，将直线x=my+$\sqrt{3}$代入椭圆方程$\frac{{x}^{2}}{4}+{y}^{2}=1$得（m2+4）y2+2$\sqrt{3}$my-1=0，求得面积，利用均值不等式求得取值范围．
解答 解：（Ⅰ）因为a=2，$\frac{b}{a}=\frac{1}{2}$，所以b=1，
所以椭圆方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$；
（Ⅱ）设M（x1，y1）N（x2，y2），直线MN方程为x=my+$\sqrt{3}$，将直线x=my+$\sqrt{3}$代入椭圆方程$\frac{{x}^{2}}{4}+{y}^{2}=1$得（m2+4）y2+2$\sqrt{3}$my-1=0，
则y1+y2=$\frac{-2\sqrt{3}m}{{m}^{2}+4}，{y}_{1}{y}_{2}=\frac{-1}{{m}^{2}+4}$，|y1-y2|=$\frac{4\sqrt{{m}^{2}+1}}{{m}^{2}+4}$∵x1＞0，x2＞0，∴$0≤|m|≤\sqrt{3}$；
面积S=${S}_{△{B}_{2}OM}+{S}_{△{B}_{1}ON}+{S}_{△OMN}$=$\frac{1}{2}（{x}_{1}+{x}_{2}）+\frac{\sqrt{3}}{2}|{y}_{1}-{y}_{2}|$=$\frac{1}{2}m（{y}_{1}+{y}_{2}）+\sqrt{3}+\frac{\sqrt{3}}{2}×\frac{4\sqrt{{m}^{2}+1}}{{m}^{2}+4}$
=$\frac{1}{2}m×\frac{-2\sqrt{3}m}{{m}^{2}+4}+\sqrt{3}+\frac{\sqrt{3}}{2}×\frac{4\sqrt{{m}^{2}+1}}{{m}^{2}+4}$=$\sqrt{3}+\sqrt{3}×\frac{2\sqrt{{m}^{2}+1}-{m}^{2}}{{m}^{2}+4}$
=$\frac{2\sqrt{3}（\sqrt{{m}^{2}+1}+2）}{{m}^{2}+4}$；
令t=$\sqrt{{m}^{2}+1}，1≤t≤2$，则$S=\frac{2\sqrt{3}（t+2）}{{t}^{2}+3}$=$\frac{2\sqrt{3}（t+2）}{（t+2）^{2}-4（t+2）+7}$=$\frac{2\sqrt{3}}{（t+2）+\frac{7}{t+2}-4}∈（\frac{8\sqrt{3}}{7}，\frac{3\sqrt{3}}{2}]$，
即S$∈（\frac{8\sqrt{3}}{7}，\frac{3\sqrt{3}}{2}]$．
所以四边形MNB1B2面积S的取值范围为S$∈（\frac{8\sqrt{3}}{7}，\frac{3\sqrt{3}}{2}]$．
点评 本题主要考查直线与圆锥曲线的综合问题，属中档题目，在高考中常有涉及．
