题目内容
3.设数列{an}的前n项和为Sn,并且满足an2,Sn,n成等差数列,an>0(n∈N*).(Ⅰ)写出an与an-1(n≥2)的关系式并求a1,a2,a3;
(Ⅱ)猜想{an}的通项公式,并用数学归纳法加以证明.
分析 (1)分别令n=1,2,3,列出方程组,能够求出求a1,a2,a3;
(2)猜想:an=n,由2Sn=an2+n可知,当n≥2时,2Sn-1=an-12+(n-1),所以an2=2an+an-12-1,再用数学归纳法进行证明.
解答 解:(1)∵an2,Sn,n成等差数列,∴2Sn=an2+n
∵Sn-Sn-1=an,∴$2{a}_{n}={a}_{n}^{2}-{a}_{n-1}^{2}+1$,∴$({a}_{n}-1)^{2}={a}_{n-1}^{2}$,∴an-an-1=±1
∵an>0,∴an-an-1=1
分别令n=1,2,3,得
$\left\{\begin{array}{l}{2{a}_{1}={a}_{1}^{2}+1}\\{2({a}_{1}+{a}_{2})={a}_{2}^{2}+2}\\{2({a}_{1}+{a}_{2}+{a}_{3})={a}_{3}^{2}+2}\end{array}\right.$∵an>0,∴a1=1,a2=2,a3=3.
(2)由(1)的结论:猜想an=n
(ⅰ)当n=1时,a1=1成立;
(ⅱ)假设当n=k(k≥2)时,ak=k.
那么当n=k+1时,
[ak+1-(k+1)][ak+1+(k-1)]=0,
∵ak+1>0,k≥2,∴ak+1+(k-1)>0,
∴ak+1=k+1.
这就是说,当n=k+1时也成立,
∴an=n(n≥2).显然n=1时,也适合.
综合(1)(2)可知对于n∈N*,an=n都成立.
点评 本题主要考查数学归纳法的应用,由数列的前n项和求通项公式,属于中档题.

练习册系列答案
相关题目
18.在平行六面体ABCD-A1B1C1D1中,若AA1=AB=AD=1,∠A1AD=∠A1AB=∠BAD=60°,则直线AC1与平面ABCD所成的角的余弦值为( )
| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
12.复数z满足(1+i)z=3+i,则复数z在复平面内所对应的点的坐标是( )
| A. | (1,-2) | B. | (-2,1) | C. | (-1,2) | D. | (2,-1) |
13.已知f(x)=sin(2015x+$\frac{3π}{8}$)+sin(2015x-$\frac{π}{8}$)的最大值为A,若存在实数x1,x2,使得对任意实数x总有f(x1)≤f(x)≤f(x2)成立,则A|x1-x2|的最小值为( )
| A. | $\frac{\sqrt{2}π}{2015}$ | B. | $\frac{2\sqrt{2}π}{2015}$ | C. | $\frac{2π}{2015}$ | D. | $\frac{4π}{2015}$ |
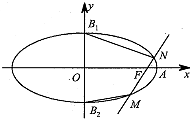 已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),其右顶点为 A(2,0),上、下顶点分别为 B1,B2.直线 A B2的斜率为$\frac{1}{2}$,过椭圆的右焦点F的直线交椭圆于 M,N两点( M,N均在y轴右侧).
已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),其右顶点为 A(2,0),上、下顶点分别为 B1,B2.直线 A B2的斜率为$\frac{1}{2}$,过椭圆的右焦点F的直线交椭圆于 M,N两点( M,N均在y轴右侧).