��Ŀ����
6����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����ҽ�����������y2=8$\sqrt{6}$x�Ľ����غϣ�����ԲC��������e=$\frac{\sqrt{6}}{3}$����������ԲC�ı����̣�
������ֱ��x=t��t��0������ԲC���ڲ�ͬ������A��B�����߶�ABΪֱ����ԲM����ԲM��y�����У���ֱ��x-$\sqrt{3}$y+1=0��ԲM���صõ��ҳ���
���� ������������${y}^{2}=8\sqrt{6}x$�Ľ�������Ϊ��$2\sqrt{6}��0$�����õ�c=$2\sqrt{6}$������������֪���ʵ���Բ���̣�
����������֪M��Բ��MΪ�߶�AB�е㣬��λ��x��������ᣬ����M������Ϊ��t��0����������Բ�ĵ�ֱ�ߵþ���Ͱ뾶�Լ��ҳ���һ�빹��ֱ�������Σ����ù��ɶ������
��� �⣺������Ϊ������${y}^{2}=8\sqrt{6}x$�Ľ�������Ϊ��$2\sqrt{6}��0$��������c=$2\sqrt{6}$������2�֣�
����Բ��������$e=\frac{c}{a}=\frac{2\sqrt{6}}{a}=\frac{\sqrt{6}}{3}$������a=6��b2=a2-c2=12
������Բ����Ϊ��$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{12}=1$������5�֣�
����������֪M��Բ��MΪ�߶�AB�е㣬��λ��x��������ᣬ����M������Ϊ��t��0��
��ΪԲM��y�����У��������B�ڵ�һ���ޣ���MA=MB=t������B��t��t��
��$\frac{{t}^{2}}{36}+\frac{{t}^{2}}{12}=1��t��0��$ ���t=3������8�֣�
��Բ��M��3��0�����뾶r=3
��ԲM�ķ���Ϊ����x-3��2+y2=9������10�֣�
��Բ��M��ֱ��x-$\sqrt{3}$y+1=0�ľ���$d=\frac{|3-0+1|}{2}=2$
���ԣ�ֱ��x-$\sqrt{3}$y+1=0��ԲM���صõ��ҳ�Ϊ��
$2\sqrt{{r}^{2}-{d}^{2}}=2\sqrt{9-4}=2\sqrt{5}$�� ����13�֣�
���� ������Ҫ����ֱ����Բ���ߣ�����Բ�����ۺ�Ӧ�ã������е����ͣ��ڸ߿��Ŀ��г����漰��

 ��ͼ������б���⻭�������ġ�ABO��ֱ��ͼ����֪O��B��=4���ҡ�ABO�����Ϊ16����A����A��C���x���ᣬ��A��C��ij�Ϊ��������
��ͼ������б���⻭�������ġ�ABO��ֱ��ͼ����֪O��B��=4���ҡ�ABO�����Ϊ16����A����A��C���x���ᣬ��A��C��ij�Ϊ��������| A�� | $2\sqrt{2}$ | B�� | $\sqrt{2}$ | C�� | $16\sqrt{2}$ | D�� | 1 |
| A�� | $\frac{{\sqrt{2}}}{3}$ | B�� | $\frac{{2\sqrt{2}}}{3}$ | C�� | $\frac{{\sqrt{3}}}{3}$ | D�� | $\frac{{\sqrt{6}}}{3}$ |
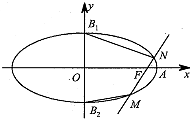 ��֪��Բ$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0�������Ҷ���Ϊ A��2��0�����ϡ��¶���ֱ�Ϊ B1��B2��ֱ�� A B2��б��Ϊ$\frac{1}{2}$������Բ���ҽ���F��ֱ�߽���Բ�� M��N���㣨 M��N����y���Ҳࣩ��
��֪��Բ$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0�������Ҷ���Ϊ A��2��0�����ϡ��¶���ֱ�Ϊ B1��B2��ֱ�� A B2��б��Ϊ$\frac{1}{2}$������Բ���ҽ���F��ֱ�߽���Բ�� M��N���㣨 M��N����y���Ҳࣩ��