题目内容
(本题满分16分)已知数列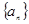 中,
中,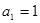 ,
, 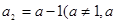 为实常数),前
为实常数),前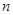 项和
项和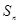 恒为正值,且当
恒为正值,且当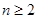 时,
时,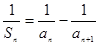 .
.
⑴求证:数列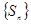 是等比数列;
是等比数列;
⑵设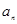 与
与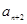 的等差中项为
的等差中项为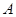 ,比较
,比较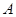 与
与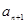 的大小;
的大小;
⑶设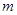 是给定的正整数,
是给定的正整数,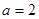 .现按如下方法构造项数为
.现按如下方法构造项数为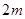 有穷数列
有穷数列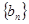 :
:
当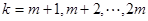 时,
时,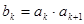 ;
;
当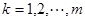 时,
时,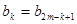 .
.
求数列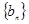 的前
的前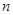 项和
项和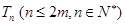 .
.
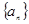 中,
中,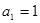 ,
, 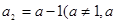 为实常数),前
为实常数),前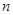 项和
项和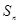 恒为正值,且当
恒为正值,且当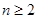 时,
时,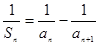 .
.⑴求证:数列
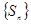 是等比数列;
是等比数列;⑵设
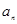 与
与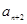 的等差中项为
的等差中项为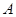 ,比较
,比较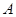 与
与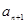 的大小;
的大小;⑶设
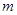 是给定的正整数,
是给定的正整数,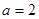 .现按如下方法构造项数为
.现按如下方法构造项数为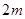 有穷数列
有穷数列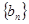 :
:当
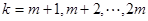 时,
时,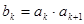 ;
;当
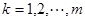 时,
时,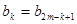 .
.求数列
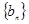 的前
的前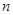 项和
项和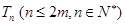 .
.(本题满分16分)
解:⑴当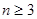 时,
时, 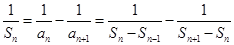 ,
,
化简得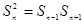
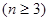 , .………………………2分
, .………………………2分
又由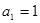 ,
,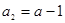 得
得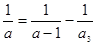 , 解得
, 解得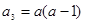 ,
,
∴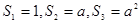 ,也满足
,也满足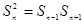 , .………………………4分
, .………………………4分
而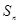 恒为正值, ∴数列
恒为正值, ∴数列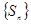 是等比数列. .………………………5分
是等比数列. .………………………5分
⑵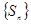 的首项为1,公比为
的首项为1,公比为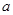 ,
,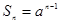 .当
.当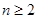 时,
时,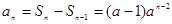 ,
,
∴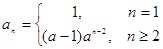 .
.
当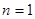 时,
时,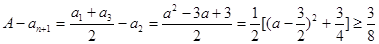 ,
,
此时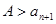 . .……………………7分
. .……………………7分
当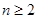 时,
时, 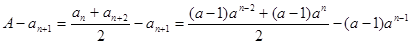
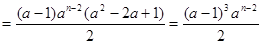 .
.
∵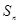 恒为正值∴
恒为正值∴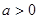 且
且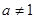 ,
,
若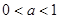 ,则
,则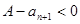 , 若
, 若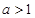 ,则
,则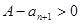 . .……………………10分
. .……………………10分
综上可得,当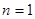 时,
时, 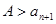 ;
;
当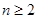 时,若
时,若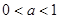 ,则
,则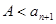 , 若
, 若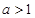 ,则
,则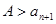 .……………………11分
.……………………11分
⑶∵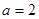 ∴
∴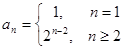 ,当
,当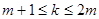 时,
时, 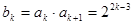 .
.
若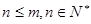 ,则由题设得
,则由题设得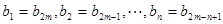
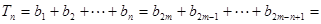
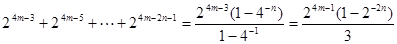 ..……………………13分若
..……………………13分若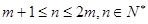 ,则
,则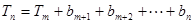
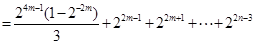
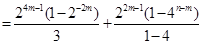
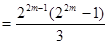 .
.
综上得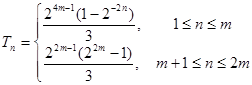 . .………………………16分
. .………………………16分
解:⑴当
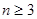 时,
时, 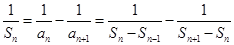 ,
,化简得
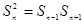
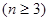 , .………………………2分
, .………………………2分又由
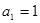 ,
,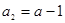 得
得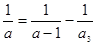 , 解得
, 解得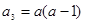 ,
,∴
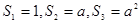 ,也满足
,也满足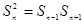 , .………………………4分
, .………………………4分而
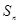 恒为正值, ∴数列
恒为正值, ∴数列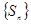 是等比数列. .………………………5分
是等比数列. .………………………5分⑵
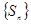 的首项为1,公比为
的首项为1,公比为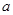 ,
,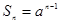 .当
.当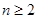 时,
时,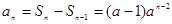 ,
, ∴
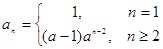 .
.当
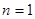 时,
时,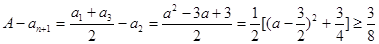 ,
,此时
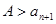 . .……………………7分
. .……………………7分 当
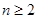 时,
时, 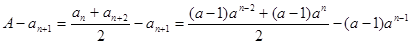
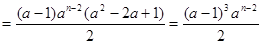 .
.∵
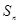 恒为正值∴
恒为正值∴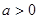 且
且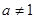 ,
,若
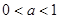 ,则
,则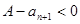 , 若
, 若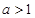 ,则
,则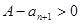 . .……………………10分
. .……………………10分综上可得,当
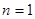 时,
时, 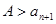 ;
;当
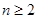 时,若
时,若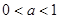 ,则
,则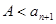 , 若
, 若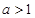 ,则
,则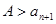 .……………………11分
.……………………11分⑶∵
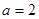 ∴
∴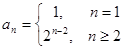 ,当
,当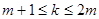 时,
时, 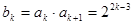 .
.若
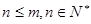 ,则由题设得
,则由题设得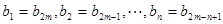
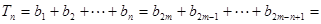
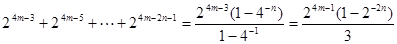 ..……………………13分若
..……………………13分若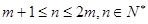 ,则
,则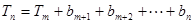
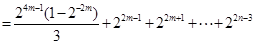
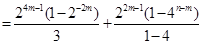
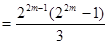 .
.综上得
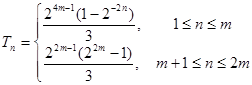 . .………………………16分
. .………………………16分略

练习册系列答案
相关题目
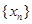 ,如果存在一个正整数
,如果存在一个正整数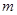 ,使得对任意的
,使得对任意的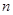 (
(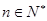 )都有
)都有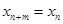 成立,那么就把这样一类数列
成立,那么就把这样一类数列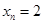 时
时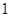 的周期数列,当
的周期数列,当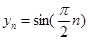 时
时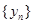 是周期为
是周期为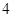 的周期数列.
的周期数列. 满足
满足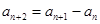 (
(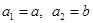 (
(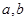 不同时为0),求证:数列
不同时为0),求证:数列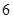 的周期数列,并求数列
的周期数列,并求数列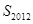 ;
;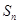 ,且
,且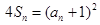 .
. 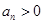 ,试判断数列
,试判断数列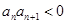 ,试判断数列
,试判断数列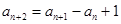 (
(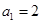 ,
,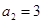 ,数列
,数列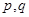 ,使对任意的
,使对任意的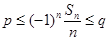 成立,若存在,求出
成立,若存在,求出 ;不存在,说明理由.
;不存在,说明理由.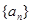 的前
的前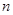 项和为
项和为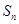 ,已知
,已知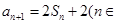 N
N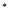 ).
). 求数列
求数列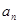 与
与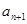 之间插入n个数,使这n+2个数组成公差为
之间插入n个数,使这n+2个数组成公差为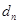 的等差数列,求数列
的等差数列,求数列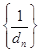 的前
的前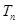 .
.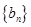 中的
中的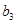 ,
,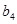 ,
,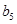 .
.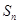 ,求证:数列
,求证:数列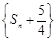 是等比数列.
是等比数列.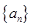 是公差为正数的等差数列,若
是公差为正数的等差数列,若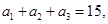
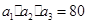 ,
,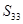 。
。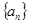 的前n项和为
的前n项和为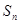 ,若
,若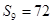 ,求
,求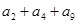 的值是( )
的值是( )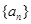 的前n项和
的前n项和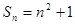 ,则
,则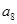 的值为
的值为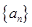 的前
的前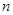 项和为
项和为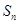 ,若
,若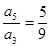 则
则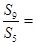
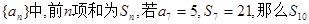 等于( )
等于( )