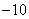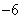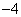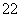题目内容
(本题满分16分)
对于数列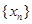 ,如果存在一个正整数
,如果存在一个正整数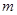 ,使得对任意的
,使得对任意的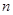 (
(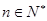 )都有
)都有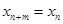 成立,那么就把这样一类数列
成立,那么就把这样一类数列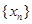 称作周期为
称作周期为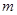 的周期数列,
的周期数列,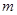 的最小值称作数列
的最小值称作数列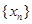 的最小正周期,以下简称周期.例如当
的最小正周期,以下简称周期.例如当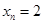 时
时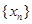 是周期为
是周期为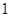 的周期数列,当
的周期数列,当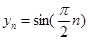 时
时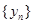 是周期为
是周期为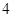 的周期数列.
的周期数列.
(1)设数列 满足
满足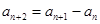 (
(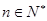 ),
),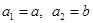 (
(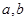 不同时为0),求证:数列
不同时为0),求证:数列 是周期为
是周期为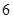 的周期数列,并求数列
的周期数列,并求数列 的前2012项的和
的前2012项的和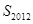 ;
;
(2)设数列 的前
的前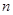 项和为
项和为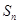 ,且
,且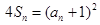 .
.
①若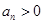 ,试判断数列
,试判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
②若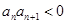 ,试判断数列
,试判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
(3)设数列 满足
满足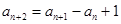 (
(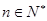 ),
),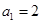 ,
,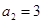 ,数列
,数列 的前
的前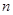 项和为
项和为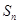 ,试问是否存在实数
,试问是否存在实数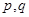 ,使对任意的
,使对任意的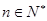 都有
都有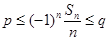 成立,若存在,求出
成立,若存在,求出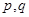 的取值范围
的取值范围 ;不存在,说明理由.
;不存在,说明理由.
对于数列
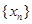 ,如果存在一个正整数
,如果存在一个正整数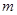 ,使得对任意的
,使得对任意的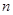 (
(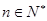 )都有
)都有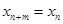 成立,那么就把这样一类数列
成立,那么就把这样一类数列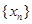 称作周期为
称作周期为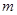 的周期数列,
的周期数列,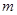 的最小值称作数列
的最小值称作数列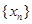 的最小正周期,以下简称周期.例如当
的最小正周期,以下简称周期.例如当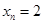 时
时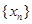 是周期为
是周期为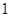 的周期数列,当
的周期数列,当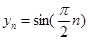 时
时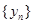 是周期为
是周期为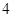 的周期数列.
的周期数列.(1)设数列
 满足
满足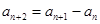 (
(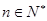 ),
),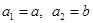 (
(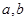 不同时为0),求证:数列
不同时为0),求证:数列 是周期为
是周期为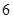 的周期数列,并求数列
的周期数列,并求数列 的前2012项的和
的前2012项的和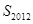 ;
;(2)设数列
 的前
的前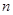 项和为
项和为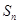 ,且
,且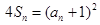 .
. ①若
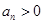 ,试判断数列
,试判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;②若
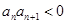 ,试判断数列
,试判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;(3)设数列
 满足
满足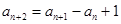 (
(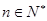 ),
),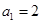 ,
,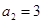 ,数列
,数列 的前
的前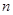 项和为
项和为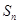 ,试问是否存在实数
,试问是否存在实数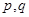 ,使对任意的
,使对任意的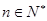 都有
都有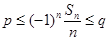 成立,若存在,求出
成立,若存在,求出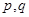 的取值范围
的取值范围 ;不存在,说明理由.
;不存在,说明理由.(1)证明: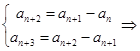
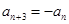 又
又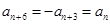 ,
,
所以 是周期为6的周期数列,………………2分
是周期为6的周期数列,………………2分
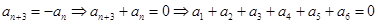 .
.
所以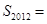
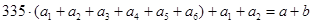 .………4分
.………4分
解:(2)当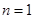 时,
时,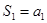 ,又
,又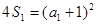 得
得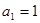 .………6分
.………6分
当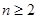 时,
时,
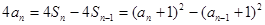
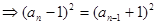 ,
,
即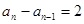 或
或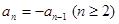 .…………6分
.…………6分
①由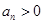 有
有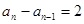
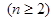 ,则
,则 为等差数列,即
为等差数列,即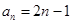 ,
,
由于对任意的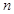 都有
都有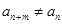 ,所以
,所以 不是周期数列.…………8分
不是周期数列.…………8分
②由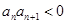 有
有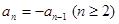 ,数列
,数列 为等比数列,即
为等比数列,即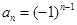 ,
,
存在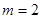 使得
使得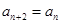 对任意
对任意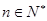 都
都 成立,
成立,
即当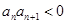 时
时 是周期为2的周期数列.…………10分
是周期为2的周期数列.…………10分
(3)假设存在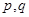 ,满足题设.
,满足题设.
于是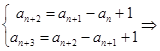
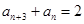 又
又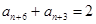 即
即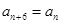 ,
,
所以 是周期为6的周期数列,
是周期为6的周期数列, 的前6项分别为
的前6项分别为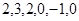 ,…12分
,…12分
则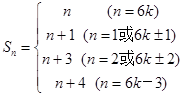 (
(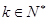 ),……14分
),……14分
当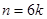 时,
时,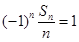 ,
,
当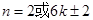 时,
时,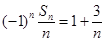
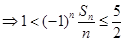 ,
,
当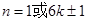 时,
时,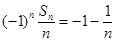
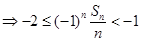 ,
,
当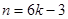 时,
时,
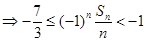 ,
,
所以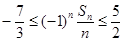 ,为使
,为使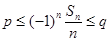 恒成立,只要
恒成立,只要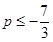 ,
,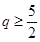 即可,
即可,
综上,假设存在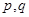 ,满足题设,
,满足题设,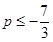 ,
,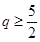 .……16分
.……16分
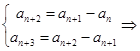
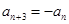 又
又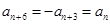 ,
,所以
 是周期为6的周期数列,………………2分
是周期为6的周期数列,………………2分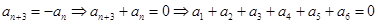 .
.所以
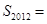
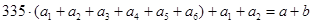 .………4分
.………4分解:(2)当
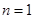 时,
时,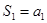 ,又
,又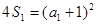 得
得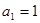 .………6分
.………6分当
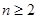 时,
时,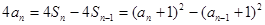
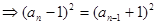 ,
,即
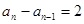 或
或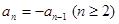 .…………6分
.…………6分①由
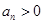 有
有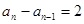
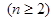 ,则
,则 为等差数列,即
为等差数列,即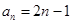 ,
,由于对任意的
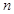 都有
都有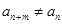 ,所以
,所以 不是周期数列.…………8分
不是周期数列.…………8分②由
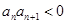 有
有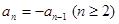 ,数列
,数列 为等比数列,即
为等比数列,即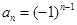 ,
,存在
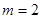 使得
使得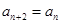 对任意
对任意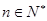 都
都 成立,
成立,即当
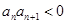 时
时 是周期为2的周期数列.…………10分
是周期为2的周期数列.…………10分(3)假设存在
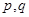 ,满足题设.
,满足题设.于是
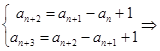
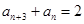 又
又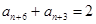 即
即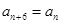 ,
,所以
 是周期为6的周期数列,
是周期为6的周期数列, 的前6项分别为
的前6项分别为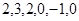 ,…12分
,…12分则
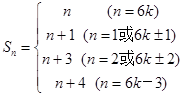 (
(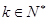 ),……14分
),……14分当
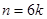 时,
时,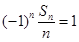 ,
,当
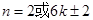 时,
时,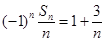
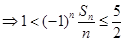 ,
,当
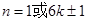 时,
时,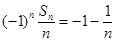
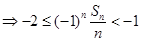 ,
,当
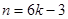 时,
时,
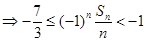 ,
,所以
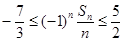 ,为使
,为使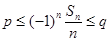 恒成立,只要
恒成立,只要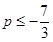 ,
,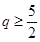 即可,
即可,综上,假设存在
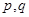 ,满足题设,
,满足题设,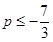 ,
,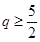 .……16分
.……16分略

练习册系列答案
相关题目
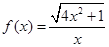 (x≠0)各项均为正数的数列{an}中a1=1,
(x≠0)各项均为正数的数列{an}中a1=1,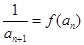 ,
,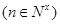 。(1)求数列{an}的通项公式;(2)在数列{bn}中,对任意的正整数n,bn·
。(1)求数列{an}的通项公式;(2)在数列{bn}中,对任意的正整数n,bn·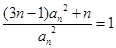 都成立,设Sn为数列{bn}的前n项和试比较Sn与
都成立,设Sn为数列{bn}的前n项和试比较Sn与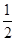 的大小。
的大小。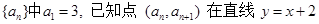 上,
上,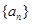 的通项公式;
的通项公式; 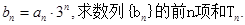
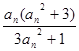
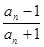 ,求证:数列{lnbn}是等比数列,并求数列{bn}的通项.
,求证:数列{lnbn}是等比数列,并求数列{bn}的通项.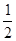
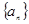 中,
中,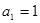 ,
, 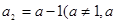 为实常数),前
为实常数),前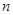 项和
项和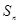 恒为正值,且当
恒为正值,且当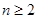 时,
时,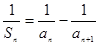 .
.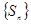 是等比数列;
是等比数列;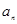 与
与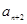 的等差中项为
的等差中项为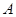 ,比较
,比较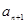 的大小;
的大小;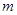 是给定的正整数,
是给定的正整数,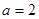 .现按如下方法构造项数为
.现按如下方法构造项数为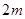 有穷数列
有穷数列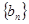 :
: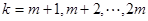 时,
时,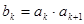 ;
;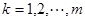 时,
时,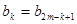 .
.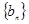 的前
的前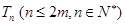 .
.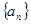 中,
中,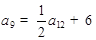 ,则数列
,则数列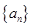 的首项为
的首项为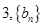 为等差数列且
为等差数列且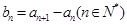 ,若
,若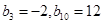 ,则
,则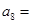 ( )
( )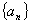 的公差为
的公差为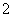 ,若
,若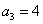 ,则第12项是 ( )
,则第12项是 ( )