题目内容
(本小题满分12分)设椭圆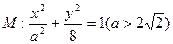 焦点坐标为F1(-c,0), F2(c,0),点Q是椭圆短轴上的顶点,且满足
焦点坐标为F1(-c,0), F2(c,0),点Q是椭圆短轴上的顶点,且满足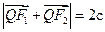 .
.
(1)求椭圆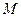 的方程;
的方程;
(2)设A,B是圆与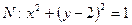 与y轴的交点,
与y轴的交点,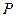 是椭圆
是椭圆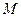 上的任一点,求
上的任一点,求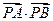 的最大值.
的最大值.
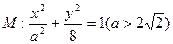 焦点坐标为F1(-c,0), F2(c,0),点Q是椭圆短轴上的顶点,且满足
焦点坐标为F1(-c,0), F2(c,0),点Q是椭圆短轴上的顶点,且满足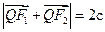 .
.(1)求椭圆
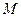 的方程;
的方程;(2)设A,B是圆与
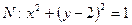 与y轴的交点,
与y轴的交点,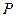 是椭圆
是椭圆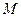 上的任一点,求
上的任一点,求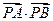 的最大值.
的最大值.(1)

(2)21
解:(1) , …………………………2分
, …………………………2分
故a2=8+8=16,故椭圆方程为: . …………………………4分
. …………………………4分
(2)令x=0,得y=3或y=1.故A(0,3),B(0,1).…………………………5分
设P(x,y),则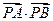 =(-x,3-y)·(-x,1-y)="x2+(3-y)(1-y)=" x2+y2-4y+3.…………7分
=(-x,3-y)·(-x,1-y)="x2+(3-y)(1-y)=" x2+y2-4y+3.…………7分
又 ,故x2="16-2" y2. …………………………8分
,故x2="16-2" y2. …………………………8分
所以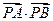 ="16-2" y2+y2-4y+3=-2(y+1)2+21 …………………………10分
="16-2" y2+y2-4y+3=-2(y+1)2+21 …………………………10分
又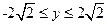 ,故y=-1时,
,故y=-1时,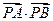 取最大值21.…………………………12分
取最大值21.…………………………12分
 , …………………………2分
, …………………………2分故a2=8+8=16,故椭圆方程为:
 . …………………………4分
. …………………………4分(2)令x=0,得y=3或y=1.故A(0,3),B(0,1).…………………………5分
设P(x,y),则
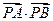 =(-x,3-y)·(-x,1-y)="x2+(3-y)(1-y)=" x2+y2-4y+3.…………7分
=(-x,3-y)·(-x,1-y)="x2+(3-y)(1-y)=" x2+y2-4y+3.…………7分又
 ,故x2="16-2" y2. …………………………8分
,故x2="16-2" y2. …………………………8分所以
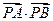 ="16-2" y2+y2-4y+3=-2(y+1)2+21 …………………………10分
="16-2" y2+y2-4y+3=-2(y+1)2+21 …………………………10分又
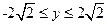 ,故y=-1时,
,故y=-1时,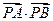 取最大值21.…………………………12分
取最大值21.…………………………12分
练习册系列答案
相关题目
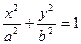 (a>b>0)
(a>b>0) ,一条准线方程为x=4 时,求椭圆方程;
,一条准线方程为x=4 时,求椭圆方程;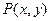 是椭圆上一点,在(1)的条件下,求
是椭圆上一点,在(1)的条件下,求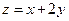 的最大值及相应的P点坐标。
的最大值及相应的P点坐标。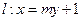 过椭圆
过椭圆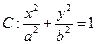 的右焦点
的右焦点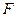 ,抛物线:
,抛物线: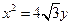 的焦点为椭圆
的焦点为椭圆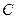 的上顶点,且直线
的上顶点,且直线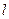 交椭圆
交椭圆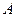 、
、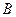 两点,点
两点,点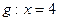 上的射影依次为点
上的射影依次为点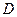 、
、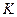 、
、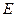 .
.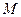 ,且
,且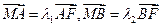 ,当
,当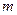 变化时,探求
变化时,探求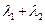 的值是否为定值?若是,求出
的值是否为定值?若是,求出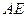 、
、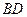 ,试探索当
,试探索当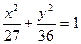 有相同焦点,且经过点
有相同焦点,且经过点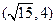 .
.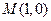 作斜率为1的直线交双曲线于
作斜率为1的直线交双曲线于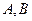 两点,求
两点,求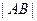 .
.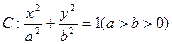 经过点(0,1),离心率
经过点(0,1),离心率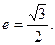
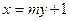 与椭圆C交于A,B两点,点A关于x轴的对称点为A’.试问:当m变化时直线
与椭圆C交于A,B两点,点A关于x轴的对称点为A’.试问:当m变化时直线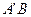 与x轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由。
与x轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由。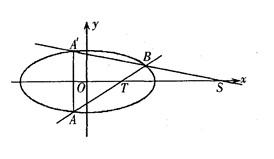
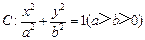 的离心率为
的离心率为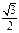 ,过右焦点
,过右焦点 且斜
且斜 率为
率为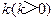 的直线与
的直线与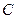 相交于
相交于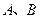 两点.若
两点.若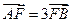 ,则
,则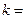 ▲
▲ 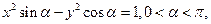 表示焦点在
表示焦点在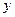 轴上的椭圆,则
轴上的椭圆,则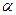 的取值范围是______ _____
的取值范围是______ _____ 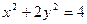 ,则以
,则以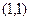 为中点的弦的长度为
为中点的弦的长度为 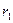 ,
, ,则卫星轨道的离心率为 .
,则卫星轨道的离心率为 .