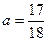题目内容
已知抛物线C: y=-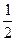 x2+6, 点P(2, 4)、A、B在抛物线上, 且直线PA、PB的倾斜角互补.
x2+6, 点P(2, 4)、A、B在抛物线上, 且直线PA、PB的倾斜角互补.
(Ⅰ)证明:直线AB的斜率为定值;
(Ⅱ)当直线AB在y轴上的截距为正数时, 求△PAB面积的最大值及此时直线AB的方程.
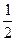 x2+6, 点P(2, 4)、A、B在抛物线上, 且直线PA、PB的倾斜角互补.
x2+6, 点P(2, 4)、A、B在抛物线上, 且直线PA、PB的倾斜角互补.(Ⅰ)证明:直线AB的斜率为定值;
(Ⅱ)当直线AB在y轴上的截距为正数时, 求△PAB面积的最大值及此时直线AB的方程.
(1)kAB=2.(2)方程为y=2x+ .
.
 .
.(Ⅰ)证: 易知点P在抛物线C上, 设PA的斜率为k, 则直线PA的方程是y-4=k(x-2).
代入y=-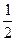 x2+6并整理得x2+2kx-4(k+1)=0此时方程应有根xA及2,
x2+6并整理得x2+2kx-4(k+1)=0此时方程应有根xA及2,
由韦达定理得:
2xA="-4(k+1)" , ∴xA="-2(k+1)." ∴yA=k(xA-2)+4.=-k2-4k+4. ∴A(-2(k+1), -k2-4k+4).
由于PA与PB的倾斜角互补, 故PB的斜率为-k.
同理可得B(-2(-k+1), -k2+4k+4)
∴kAB="2."
(Ⅱ) ∵AB的方程为y="2x+b," b>0.代入方程y=-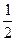 x2+6消去y得
x2+6消去y得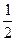 x2+2x+b-6=0.
x2+2x+b-6=0.
|AB|=2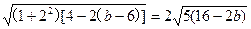 .
.
∴S=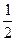 |AB|d=
|AB|d=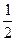 ·2
·2
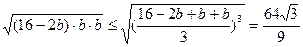 .
.
此时方程为y=2x+ .
.
代入y=-
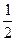 x2+6并整理得x2+2kx-4(k+1)=0此时方程应有根xA及2,
x2+6并整理得x2+2kx-4(k+1)=0此时方程应有根xA及2, 由韦达定理得:
2xA="-4(k+1)" , ∴xA="-2(k+1)." ∴yA=k(xA-2)+4.=-k2-4k+4. ∴A(-2(k+1), -k2-4k+4).
由于PA与PB的倾斜角互补, 故PB的斜率为-k.
同理可得B(-2(-k+1), -k2+4k+4)
∴kAB="2."
(Ⅱ) ∵AB的方程为y="2x+b," b>0.代入方程y=-
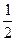 x2+6消去y得
x2+6消去y得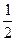 x2+2x+b-6=0.
x2+2x+b-6=0.|AB|=2
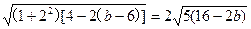 .
. ∴S=
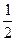 |AB|d=
|AB|d=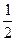 ·2
·2
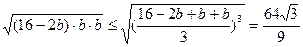 .
. 此时方程为y=2x+
 .
.
练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
 是坐标原点,
是坐标原点, 是抛物线
是抛物线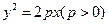 的焦点,
的焦点,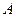 是抛物线上的一点,
是抛物线上的一点,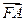 与
与 轴正向的夹角为
轴正向的夹角为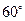 ,则
,则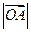 为 ( )
为 ( )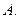

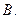
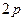
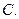
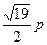

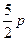
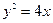 上一点,且在
上一点,且在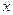 轴上
轴上 方,F是抛物线的焦
方,F是抛物线的焦 点,以
点,以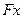 为始边,FM为终边的角
为始边,FM为终边的角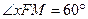 ,则
,则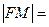
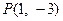 的抛物线的标准方程是
的抛物线的标准方程是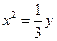 或
或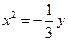
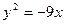 或
或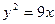
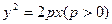 的焦点
的焦点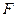 的直线
的直线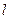 与抛物线在第一象限的交点为A,与抛物线的准线的交点为
与抛物线在第一象限的交点为A,与抛物线的准线的交点为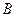 ,点
,点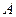 在抛物线的准线上的射影为
在抛物线的准线上的射影为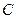 ,若
,若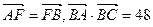 ,则抛物线的方程为 ( )
,则抛物线的方程为 ( )

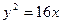

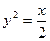 与圆
与圆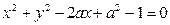 有且只有三个公共点,则a的取值范围是( )
有且只有三个公共点,则a的取值范围是( )