题目内容
如图,已知三棱柱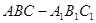 的侧棱与底面垂直,
的侧棱与底面垂直,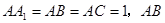 ⊥AC,M是
⊥AC,M是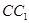 的中点,N是BC的中点,点P在直线
的中点,N是BC的中点,点P在直线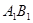 上,且满足
上,且满足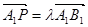 .
.
(1)当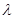 取何值时,直线PN与平面ABC所成的角
取何值时,直线PN与平面ABC所成的角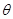 最大?
最大?
(2)若平面PMN与平面ABC所成的二面角为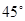 ,试确定点P的位置.
,试确定点P的位置.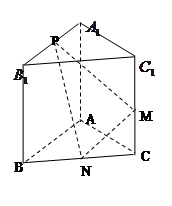
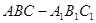 的侧棱与底面垂直,
的侧棱与底面垂直,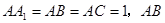 ⊥AC,M是
⊥AC,M是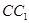 的中点,N是BC的中点,点P在直线
的中点,N是BC的中点,点P在直线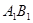 上,且满足
上,且满足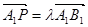 .
.(1)当
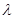 取何值时,直线PN与平面ABC所成的角
取何值时,直线PN与平面ABC所成的角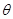 最大?
最大?(2)若平面PMN与平面ABC所成的二面角为
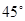 ,试确定点P的位置.
,试确定点P的位置.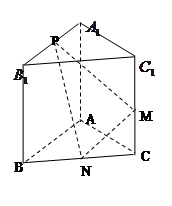
(1)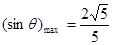 (2)
(2)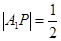
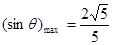 (2)
(2)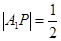
本试题主要考查了立体几何中线面角以及二面角的求解和运用。
解:(1)以AB,AC,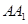 分别为
分别为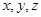 轴,建立空间直角坐标系
轴,建立空间直角坐标系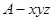 ,则
,则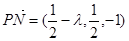 ,平面ABC的一个法向量为
,平面ABC的一个法向量为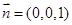 …………2分
…………2分
则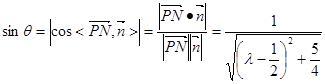 …………………5分
…………………5分
于是问题转化为二次函数求最值,而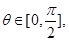 当
当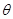 最大时,
最大时,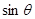 最大,所以当
最大,所以当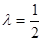 时,
时,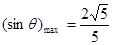 .…………………7分
.…………………7分
(2)已知给出了平面PMN与平面ABC所成的二面角为 ,即可得到平面ABC的一个法向量为
,即可得到平面ABC的一个法向量为 ,设平面PMN的一个法向量为
,设平面PMN的一个法向量为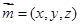 ,
,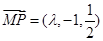 .
.
由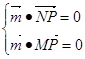 得
得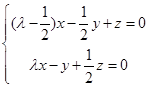 ,…………………9分
,…………………9分
解得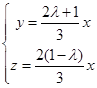 .…………………10分
.…………………10分
令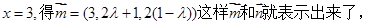 于是由
于是由
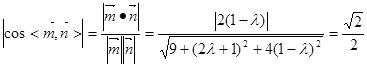 ,……………13分
,……………13分
解得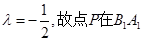 的延长线上,且
的延长线上,且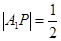 .
.
解:(1)以AB,AC,
 分别为
分别为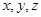 轴,建立空间直角坐标系
轴,建立空间直角坐标系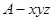 ,则
,则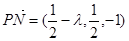 ,平面ABC的一个法向量为
,平面ABC的一个法向量为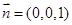 …………2分
…………2分则
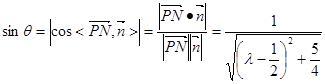 …………………5分
…………………5分于是问题转化为二次函数求最值,而
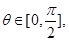 当
当 最大时,
最大时, 最大,所以当
最大,所以当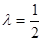 时,
时,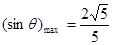 .…………………7分
.…………………7分(2)已知给出了平面PMN与平面ABC所成的二面角为
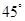 ,即可得到平面ABC的一个法向量为
,即可得到平面ABC的一个法向量为 ,设平面PMN的一个法向量为
,设平面PMN的一个法向量为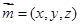 ,
,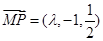 .
.由
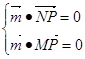 得
得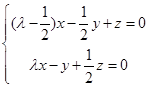 ,…………………9分
,…………………9分解得
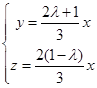 .…………………10分
.…………………10分令
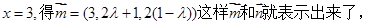 于是由
于是由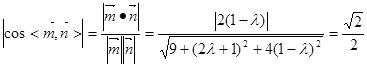 ,……………13分
,……………13分解得
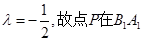 的延长线上,且
的延长线上,且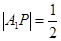 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
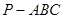 中,
中,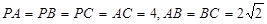
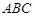 ⊥平面
⊥平面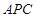
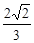 ,求BM的最小值.
,求BM的最小值.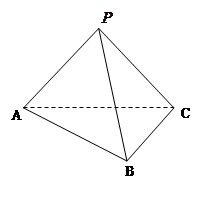
 中,底面
中,底面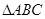 为等腰直角三角形,
为等腰直角三角形,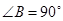 ,
,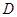 为棱
为棱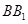 上一点,且平面
上一点,且平面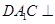 平面
平面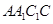 .
.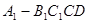 和
和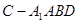 的体积是否相等,并证明。
的体积是否相等,并证明。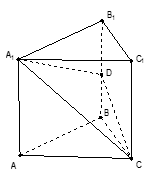
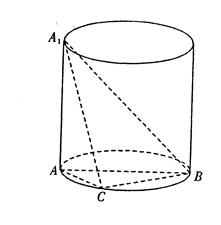
 中,已知
中,已知 ,
, ,且
,且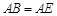 ,连接
,连接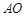 .
.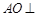 平面
平面 ;
; 为正方形.
为正方形.
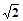 ,求AB1与C1B所成角的大小。
,求AB1与C1B所成角的大小。