题目内容
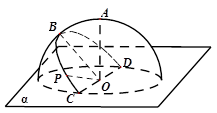
如图A1A是圆柱的母线,AB是圆柱底面圆的直径,C是底面圆周上异于A、B的任一点,AA1=AB=2
⑴求证:BC⊥平面A1AC
⑵求三棱锥A1—ABC体积的最大值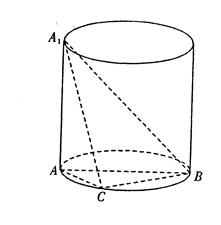
⑴求证:BC⊥平面A1AC
⑵求三棱锥A1—ABC体积的最大值

(1)见解析;(2)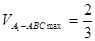 .
.
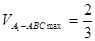 .
.(1)关键是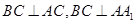 即可.
即可.
(2)由于三棱锥A1—ABC的高等于2,底面积最大时,体积最大,因为AB=2,所以当点C到直线AB的距离最大时,即点C到AB的距离等于半径时,体积最大.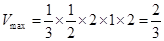 .
.
证明: (1)提示:关键是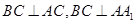 即可.
即可.
解:(2)由于三棱锥A1—ABC的高等于2,底面积最大时,体积最大,因为AB=2,所以当点C到直线AB的距离最大时,即点C到AB的距离等于半径时,体积最大.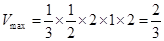 .
.
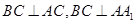 即可.
即可.(2)由于三棱锥A1—ABC的高等于2,底面积最大时,体积最大,因为AB=2,所以当点C到直线AB的距离最大时,即点C到AB的距离等于半径时,体积最大.
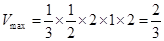 .
.证明: (1)提示:关键是
 即可.
即可.解:(2)由于三棱锥A1—ABC的高等于2,底面积最大时,体积最大,因为AB=2,所以当点C到直线AB的距离最大时,即点C到AB的距离等于半径时,体积最大.
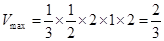 .
.
练习册系列答案
相关题目
 中,侧面
中,侧面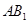 内有一动点
内有一动点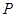 到直线
到直线 与直线
与直线 的距离相等,则动点
的距离相等,则动点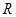 的半球
的半球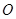 的底面圆
的底面圆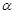 内,过点
内,过点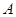 ,过圆
,过圆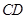 作平面
作平面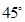 角的平面与半球面相交,所得交线上到平面
角的平面与半球面相交,所得交线上到平面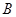 ,该交线上的一点
,该交线上的一点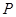 满足
满足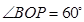 ,则
,则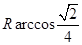
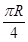
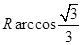
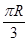
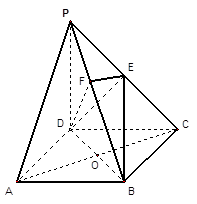
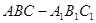 的侧棱与底面垂直,
的侧棱与底面垂直,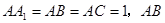 ⊥AC,M是
⊥AC,M是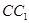 的中点,N是BC的中点,点P在直线
的中点,N是BC的中点,点P在直线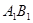 上,且满足
上,且满足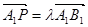 .
.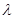 取何值时,直线PN与平面ABC所成的角
取何值时,直线PN与平面ABC所成的角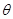 最大?
最大?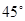 ,试确定点P的位置.
,试确定点P的位置.
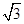 ,VC=7,画出二面角V-AB-C的平面角,并求它的余弦值。
,VC=7,画出二面角V-AB-C的平面角,并求它的余弦值。 中,二面角
中,二面角 的正切值为 ___.
的正切值为 ___.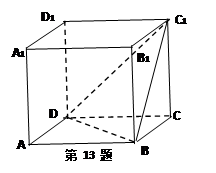
 中,若点
中,若点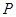 是棱上一点,则满足
是棱上一点,则满足 的点
的点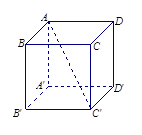
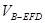 .
.
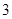 ,圆心角为
,圆心角为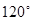 的扇形,则圆锥的底面圆半径是
的扇形,则圆锥的底面圆半径是