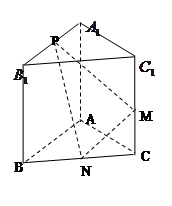题目内容
如图,在三棱锥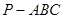 中,
中,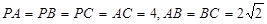
(1)求证:平面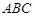 ⊥平面
⊥平面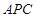
(2)求直线PA与平面PBC所成角的正弦值;
(3)若动点M在底面三角形ABC上,二面角M-PA-C的余弦值为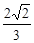 ,求BM的最小值.
,求BM的最小值.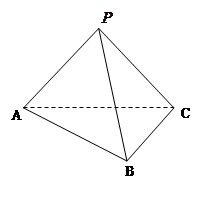
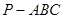 中,
中,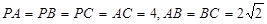
(1)求证:平面
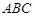 ⊥平面
⊥平面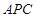
(2)求直线PA与平面PBC所成角的正弦值;
(3)若动点M在底面三角形ABC上,二面角M-PA-C的余弦值为
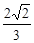 ,求BM的最小值.
,求BM的最小值.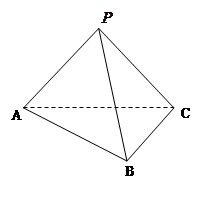
(1)见解析 (2)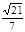 . (3)
. (3)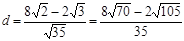 .
.
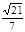 . (3)
. (3)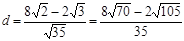 .
. (1)本题解决的关键是取线段AC中点O,利用等腰三角形和直角三角形的性质得OP⊥OC,OP⊥OB.由线面垂直的判定定理得OP⊥平面ABC,再由面面垂直的判定定理得平面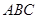 ⊥平面
⊥平面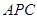 .
.
(2)由(1)得OB、OC、OP两两垂直,可以O为坐标原点建立空间直角坐标系,然后利用
空间向量法求出平面PBC的法向量,再根据直线与平面所成角的向量法求解即可.
(3)在(2)的基础上可知平面PAC的法向量,然后再求出平面PAM的法向量, 则根据这两个法向量夹角的余弦值为为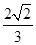 ,求出直线AM的方程,然后利用点到直线的距离公式可求出B点到AM的最小值.
,求出直线AM的方程,然后利用点到直线的距离公式可求出B点到AM的最小值.
(1)取AC中点O,因为AP=BP,所以OP⊥OC 由已知易得三角形ABC为直角三角形,∴OA=OB=OC,⊿POA≌⊿POB≌⊿POC,∴OP⊥OB
∴OP⊥平面ABC, ∵OP在平面PAC中,∴平面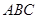 ⊥平面
⊥平面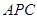 4分
4分
(2) 以O为坐标原点,OB、OC、OP分别为x、y、z轴建立如图所示空间直角坐标系.

由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0),P(0,0,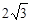 ), 5分
), 5分
∴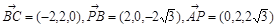 设平面PBC的法向量
设平面PBC的法向量 ,
,
由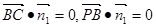 得方程组
得方程组
 ,取
,取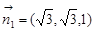 6分
6分
∴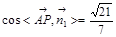
∴直线PA与平面PBC所成角的正弦值为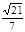 . 8分
. 8分
(3)由题意平面PAC的法向量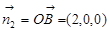 , 设平面PAM的法向量为
, 设平面PAM的法向量为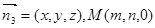 ∵
∵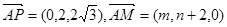 又因为
又因为
∴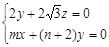 取
取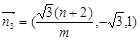
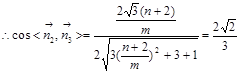
∴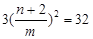 ∴
∴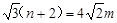 11分
11分
∴B点到AM的最小值为垂直距离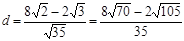 .
.
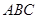 ⊥平面
⊥平面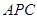 .
.(2)由(1)得OB、OC、OP两两垂直,可以O为坐标原点建立空间直角坐标系,然后利用
空间向量法求出平面PBC的法向量,再根据直线与平面所成角的向量法求解即可.
(3)在(2)的基础上可知平面PAC的法向量,然后再求出平面PAM的法向量, 则根据这两个法向量夹角的余弦值为为
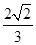 ,求出直线AM的方程,然后利用点到直线的距离公式可求出B点到AM的最小值.
,求出直线AM的方程,然后利用点到直线的距离公式可求出B点到AM的最小值.(1)取AC中点O,因为AP=BP,所以OP⊥OC 由已知易得三角形ABC为直角三角形,∴OA=OB=OC,⊿POA≌⊿POB≌⊿POC,∴OP⊥OB
∴OP⊥平面ABC, ∵OP在平面PAC中,∴平面
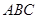 ⊥平面
⊥平面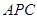 4分
4分(2) 以O为坐标原点,OB、OC、OP分别为x、y、z轴建立如图所示空间直角坐标系.

由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0),P(0,0,
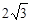 ), 5分
), 5分∴
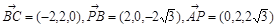 设平面PBC的法向量
设平面PBC的法向量 ,
,由
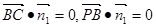 得方程组
得方程组 ,取
,取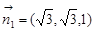 6分
6分∴
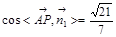
∴直线PA与平面PBC所成角的正弦值为
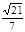 . 8分
. 8分(3)由题意平面PAC的法向量
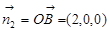 , 设平面PAM的法向量为
, 设平面PAM的法向量为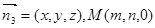 ∵
∵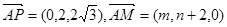 又因为
又因为
∴
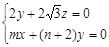 取
取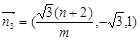
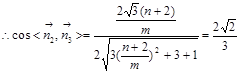
∴
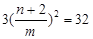 ∴
∴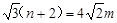 11分
11分∴B点到AM的最小值为垂直距离
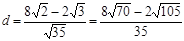 .
.
练习册系列答案
相关题目
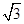 ,BD=CD=1,另一个侧面是正三角形
,BD=CD=1,另一个侧面是正三角形
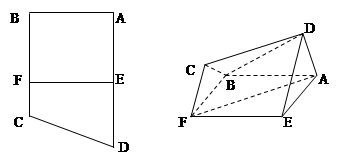
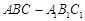 中,
中,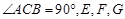 分别是
分别是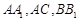 的中点,且
的中点,且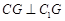 .
. 平面
平面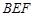 ;
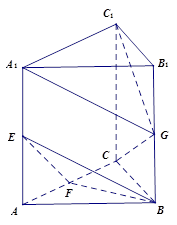
; 平面
平面 .
.
 BC,E、F分别为CD、PB的中点。
BC,E、F分别为CD、PB的中点。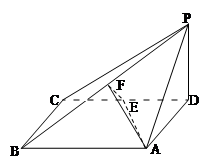
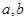 是异面直线,
是异面直线,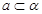 ,
,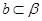 ,
,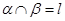 ,则下列命题中是真命题的为
,则下列命题中是真命题的为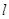 与
与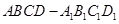 中,侧面
中,侧面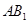 内有一动点
内有一动点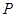 到直线
到直线 与直线
与直线 的距离相等,则动点
的距离相等,则动点
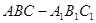 的侧棱与底面垂直,
的侧棱与底面垂直,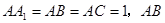 ⊥AC,M是
⊥AC,M是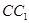 的中点,N是BC的中点,点P在直线
的中点,N是BC的中点,点P在直线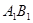 上,且满足
上,且满足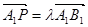 .
.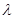 取何值时,直线PN与平面ABC所成的角
取何值时,直线PN与平面ABC所成的角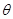 最大?
最大?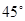 ,试确定点P的位置.
,试确定点P的位置.