题目内容
如图,已知矩形ABCD,PA⊥平面ABCD于A,M,N分别为AB,PC的中点
(1)求证:MN⊥AB;
(2)若平面PDC与平面ABCD所成的二面角为θ,能否确定θ,使直线MN是异面直线AB与PC的公垂线?若能确定,求出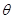 的值;若不能确定,说明理由.
的值;若不能确定,说明理由.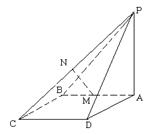
(1)求证:MN⊥AB;
(2)若平面PDC与平面ABCD所成的二面角为θ,能否确定θ,使直线MN是异面直线AB与PC的公垂线?若能确定,求出
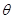 的值;若不能确定,说明理由.
的值;若不能确定,说明理由.
证明:
(1)见解析;
(2)由已知角PDA就是平面PDC与平面ABCD所成二面角平面角直角三角形PDA中设AD=a,则PD=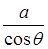 ,取CD中点G,直角三角形MNG中,角MGN=
,取CD中点G,直角三角形MNG中,角MGN=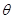 ,MG=
,MG=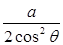 ,于是
,于是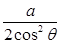 =
=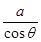 ,得
,得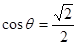 ,
,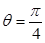 能确定
能确定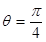 ,使MN是异面直线AB与PC的公垂线
,使MN是异面直线AB与PC的公垂线
(1)见解析;
(2)由已知角PDA就是平面PDC与平面ABCD所成二面角平面角直角三角形PDA中设AD=a,则PD=
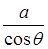 ,取CD中点G,直角三角形MNG中,角MGN=
,取CD中点G,直角三角形MNG中,角MGN=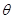 ,MG=
,MG=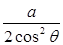 ,于是
,于是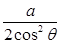 =
=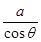 ,得
,得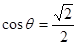 ,
,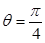 能确定
能确定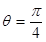 ,使MN是异面直线AB与PC的公垂线
,使MN是异面直线AB与PC的公垂线 (1)取CD中点G,连接MG,NG,则面MNG∥面PAD,易正明AB⊥面PAD,故AB⊥面MNE,进而AB⊥MN; 直线MN是异面直线AB与PC的公垂线,只需再AB⊥PC即可。
证明:
(1)略
(2)由已知角PDA就是平面PDC与平面ABCD所成
成二面角平面角直角三角形PDA中设AD=a,则PD=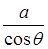
取CD中点G,直角三角形MNG中,角MGN=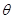 ,MG=
,MG=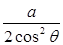
于是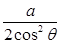 =
=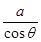 ,得
,得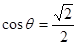 ,
,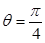 能确定
能确定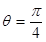 ,使MN是异面直线AB与PC的公垂线
,使MN是异面直线AB与PC的公垂线
证明:
(1)略
(2)由已知角PDA就是平面PDC与平面ABCD所成
成二面角平面角直角三角形PDA中设AD=a,则PD=
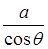
取CD中点G,直角三角形MNG中,角MGN=
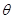 ,MG=
,MG=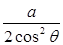
于是
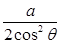 =
=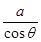 ,得
,得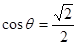 ,
,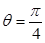 能确定
能确定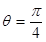 ,使MN是异面直线AB与PC的公垂线
,使MN是异面直线AB与PC的公垂线 
练习册系列答案
相关题目
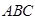
 平面
平面 ,
, 与
与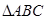 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形,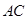 //
//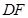 ,四边形
,四边形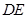 //
//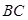 ,
,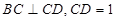 ,点
,点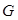 为
为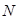 为
为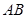 中点,
中点,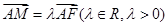 ,
,
 时,求证:
时,求证: //平面
//平面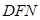
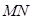 与
与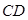 所成角为
所成角为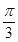 ,试求二面角
,试求二面角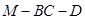 的余弦值.
的余弦值.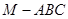 中,
中,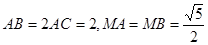 ,
,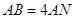 ,
,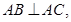 平面
平面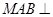 平面
平面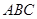 ,
,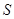 为
为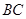 的中点.
的中点.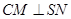 ;
;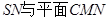 所成角的大小.
所成角的大小.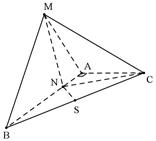
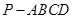 中,底面
中,底面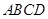 是菱形,
是菱形,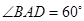 ,
,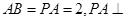 底面
底面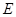 是
是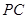 的中点,
的中点,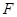 是
是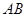 中点。
中点。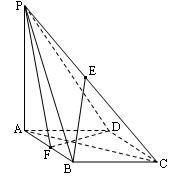
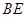 ∥平面
∥平面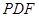 ;
;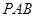 ;
;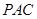 所成的角。
所成的角。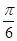 ,求证:FG⊥平面ABCD
,求证:FG⊥平面ABCD
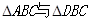 均是边长为2的等边三角形,且它们所在平面互相垂直,
均是边长为2的等边三角形,且它们所在平面互相垂直,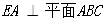 ,
,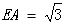 .
.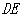 ||
|| 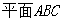
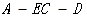 的余弦值。.
的余弦值。. 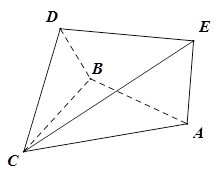
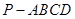 的底面
的底面 是矩形,
是矩形,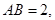
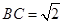 ,且侧面
,且侧面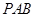 是正三角形,平面
是正三角形,平面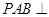 平面
平面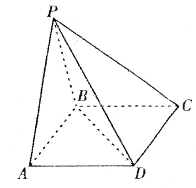
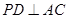 ;
;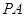 上是否存在一点
上是否存在一点 ,使得二面角
,使得二面角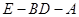 的大小为45°.若存在,试求
的大小为45°.若存在,试求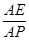 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.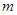 、
、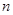 是两条不同的直线,
是两条不同的直线,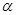 、
、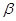 是两个不同的平面. 考察下列命题,其中真命题是
是两个不同的平面. 考察下列命题,其中真命题是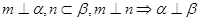
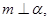
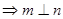
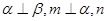 ∥
∥
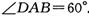 ,菱形ABCD的两条对角线的交点为0,PA=PC,PB=PD,且PO=3.点E是线段PA的中点,连接EO、EB、EC.
,菱形ABCD的两条对角线的交点为0,PA=PC,PB=PD,且PO=3.点E是线段PA的中点,连接EO、EB、EC.